浙江省温州新力量联盟2018-2019学年高二下学期数学期中考试试卷
试卷更新日期:2020-05-25 类型:期中考试
一、单选题
-
1. 已知复数 ( 是虚数单位).则复数 的虚部是( )A、 B、 C、 D、2. 函数 在 上是减函数.则( )A、 B、 C、 D、3. 下列函数中,既是奇函数,又是增函数的是( )A、 B、 C、 D、4. 已知集合 , ,则 ( )A、 B、 C、 D、5. 设 ,则函数 的零点所在的区间为( )A、(0,1) B、 C、 D、6. 已知函数 ,若 ,则实数 的值为( )A、 B、 或 C、 D、 或7. 已知函数 ,将函数 的图象向右平移 后得到函数 的图象,则下列描述正确的是( )A、 是函数 的一个对称中心 B、 是函数 的一条对称轴 C、 是函数 的一个对称中心 D、 是函数 的一条对称轴8. 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积= (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为 ,半径等于 米的弧田,按照上述经验公式计算所得弧田面积约是( )
 A、 平方米 B、 平方米 C、 平方米 D、 平方米9. 如图,函数 (其中 )与坐标轴的三个交点 满足 为 的中点, ,则 的值为( )
A、 平方米 B、 平方米 C、 平方米 D、 平方米9. 如图,函数 (其中 )与坐标轴的三个交点 满足 为 的中点, ,则 的值为( )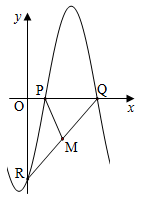 A、 B、 C、 D、10. 已知集合 ,若对于任意 ,存在 ,使得 成立,则称集合 是“理想集合”.给出下列4个集合:
A、 B、 C、 D、10. 已知集合 ,若对于任意 ,存在 ,使得 成立,则称集合 是“理想集合”.给出下列4个集合:① ;② ;③ ;④ .其中所有“理想集合”的序号是( )
A、①③ B、②③ C、②④ D、③④二、双空题
-
11. , .12. 已知向量 ,若 ,则 ;若 ,则 .13. 已知 ,则 , .14. 在边长等于1的正方形 中, 和 分别是 和 的中点,则 , 若 ,其中 ,则 .
三、填空题
-
15. 已知函数 定义域为 ,则实数 的取值范围是 .16. 设 ,且 ,则 .17. 设函数 的定义域为 ,若 ,使得 成立,则称函数 为“美丽函数”.下列所给出的五个函数:
① ;② ;③ ;④ ;⑤ .
其中是“美丽函数”的序号有 .
四、解答题