2016年云南省中考数学模拟试卷（二）

试卷更新日期：2016-04-26 类型：中考模拟

进入出卷网下载

一、选择题（本大题共8小题，每小题只有一个正确选项，每小题3分，满分24分）

1. ﹣2015的相反数是（　　）

A、﹣2015 B、 $\frac{1}{2015}$ C、2015 D、﹣ $\frac{1}{2015}$

查看试题解析
2. 下列计算错误的是（　　）

A、 $1 \div 6 \times \frac{1}{6} = \frac{1}{36}$ B、（﹣2）^﹣²=4 C、 $\frac{1}{3} - 2 - (- 2 \frac{1}{3}) = \frac{2}{3}$ D、2015⁰=1

查看试题解析
3.
如图，由4个大小相同的正方体组合而成的几何体，其俯视图是（　　）

A、 B、 C、 D、

查看试题解析
4. 不等式组 ${\begin{cases} \frac{x - 3}{2} \geq 1 \\ 8 - x ＞ 0 \end{cases}$ 的解集是（　　）

A、x≥5 B、5≤x＜8 C、x＞8 D、无解

查看试题解析
5.
如图，AB∥CD，AD平分∠BAC，且∠D=72°，则∠C的度数为（　　）

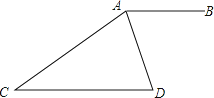A、36° B、72° C、108° D、144°

查看试题解析
6. 已知抛物线y=﹣x²+2x﹣3，下列判断正确的是（　　）

A、开口方向向上，y有最小值是﹣2 B、抛物线与x轴有两个交点 C、顶点坐标是（﹣1，﹣2） D、当x＜1时，y随x增大而增大

查看试题解析
7. 2015年4月某日我市区县的可吸入颗粒物数值统计如下表：
区县
宣威
富源
沾益
马龙
师宗
罗平
陆良
会泽
麒麟区
经开区
可吸入颗粒物
（mg/m3）
0.18
0.18
0.15
0.13
0.14
0.13
0.15
0.15
0.15
0.14
该日这一时刻的可吸入颗粒物数值的众数和中位数分别是（　　）

A、0.15和0.14 B、0.18和0.15 C、0.18和0.14 D、0.15和0.15

查看试题解析
8.
如图，△ABC中，∠C=90°，∠A=30°．分别以顶点A、B为圆心，大于 $\frac{1}{2}$ AB为半径作弧，两弧在直线AB两侧分别交于M、N两点，过M、N作直线交AB于点P，交AC于点D，连接BD．下列结论中，错误的是（　　）

A、直线AB是线段MN的垂直平分线 B、CD= $\frac{1}{2}$ AD C、BD平分∠ABC D、S_△_APD=S_△_BCD

查看试题解析

二、填空题（本大题共6个小题，每小题3分，满分18分）

9. 计算： $\sqrt{12} - \sqrt{3}$ =

查看试题解析
10. 2014年博鳌亚洲论坛年会开幕大会上，中国全面阐述了亚洲合作政策，并特别强调要推进“一带一路”的建设，中国将出资400亿美元设丝路基金．用科学记数法表示400亿美元为美元．

查看试题解析
11. 一元二次方程x²﹣4x+4=0的解是．

查看试题解析
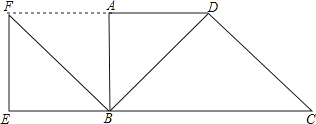
12.
如图，在△ABC中，D、E分别是边AB、AC的中点，连接DE，将△ADE沿AB方向平移到△DBF的位置，点D在BC上，已知△ADE的面积为1，则四边形CEDF的面积是．

查看试题解析
13.
在直角梯形ABCD中，AD∥BC，∠DAB=90°，AD=1，BC=2．连接BD，把△ABD绕着点B逆时针旋转90°得到△EBF，若点F刚好落在DA的延长线上，则∠C=°．

查看试题解析
14. 观察下列等式： $\frac{1}{2} = 1 - \frac{1}{2} = \frac{1}{2}$ ， $\frac{1}{2} + \frac{1}{4} = 1 - \frac{1}{4} = \frac{3}{4}$ ， $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} = 1 - \frac{1}{8} = \frac{7}{8}$ ，…则 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots$ + $\frac{1}{2^{n}}$ = ．（直接填结果，用含n的代数式表示，n是正整数，且n≥1）

查看试题解析

三、解答题（共9个小题，共58分）

15. 化简： $（ \frac{x}{x - 1} - \frac{1}{x^{2} - x}) \div \frac{x^{2} + 2 x + 1}{x^{2}}$ ，并从﹣1，0，1，2中选择一个合适的数求代数式的值．

查看试题解析
16.
如图，四边形ABCD是矩形，点E是AD的中点，点F是BC的中点．求证：△ABF≌△CDE．

查看试题解析
17.
如图，已知反比例函数 $y = \frac{k}{x}$ （k≠0）的图象过点A（﹣3，2）．

(1)、求这个反比例函数的解析式；

(2)、若B（x₁ ， y₁），C（x₂ ， y₂），D（x₃ ， y₃）是这个反比例函数图象上的三个点，若x₁＞x₂＞0＞x₃ ，请比较y₁ ， y₂ ， y₃的大小，并说明理由．

查看试题解析
18. 昆曲高速公路全长128千米，甲、乙两车同时从昆明、曲靖两地高速路收费站相向匀速开出，经过40分钟相遇，甲车比乙车每小时多行驶20千米．求甲、乙两车的速度．

查看试题解析
19. 课间小明和小亮玩“剪刀、石头、布”游戏．游戏规则是：双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种，石头胜剪刀，剪刀胜布，布胜石头，若双方出现相同手势，则算打平．若小亮和小明两人只比赛一局．

(1)、请用树状图或列表法列出游戏的所有可能结果．

(2)、求出双方打平的概率．

(3)、游戏公平吗？如果不公平，你认为对谁有利？

查看试题解析
20.
学校准备在各班设立图书角以丰富同学们的课余文化生活，为了更合理的搭配各类书籍，学校团委以“我最喜爱的书籍”为主题，对学生最喜爱的一种书籍类型进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图1和图2提供的信息，解答下列问题：

(1)、在这次抽样调查中，一共调查了多少名学生？

(2)、请把折线统计图（图1）补充完整；

(3)、求出扇形统计图（图2）中，体育部分所对应的圆心角的度数；

(4)、如果这所中学共有学生1800名，那么请你估计最喜爱科普类书籍的学生人数．

查看试题解析
21.
如图，在▱ABCD中，对角线AC、BD相交成的锐角为60°，若AC=6，BD=8，求▱ABCD的面积．（ $\sqrt{3} \approx 1.73$ ，结果精确到0.1）

查看试题解析
22.
如图，将圆形纸片沿弦AB折叠后，圆弧恰好能经过圆心O，⊙O的切线BC与AO延长线交于点C．

(1)、若⊙O半径为6cm，用扇形OAB围成一个圆锥的侧面，求这个圆锥的底面圆半径．

(2)、求证：AB=BC．

查看试题解析
23.
如图，在平面直角坐标系中，直线AB和抛物线交于点A（﹣4，0），B（0，4），且点B是抛物线的顶点．

(1)、求直线AB和抛物线的解析式．

(2)、点P是直线上方抛物线上的一点，求当△PAB面积最大时点P的坐标．

(3)、M是直线AB上一动点，在平面直角坐标系内是否存在点N，使以O、B、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．

查看试题解析