人教A版（2019）数学必修第二册 第九章 统计

试卷更新日期：2020-05-20 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 经调查，在某商场扫码支付的老年人、中年人、青年人的比例为 2:3:5 ，用分层抽样的方法抽取了一个容量为 n 的样本进行调查，其中中年人人数为9，则 n= （  ）
    A、30 B、40 C、60 D、80

    查看试题解析

  • 2. 在 30 名运动员和 6 名教练员中用分层抽样的方法共抽取 n 人参加新闻发布会，若抽取的 n 人中教练员只有 1 人，则 n= （   ）
    A、5 B、6 C、7 D、8

    查看试题解析

  • 3. 已知甲、乙两组数据用茎叶图表示如图所示，若它们的中位数相同， 平均数也相同，则图中的 m ， n 的比值 mn 等于（   ）

    A、38 B、29 C、13 D、12

    查看试题解析

  • 4. 若样本 1+x1,1+x2,1+x3,⋯,1+xn 的平均数是10，方差为2，则对于样本 2+2x1,2+2x2,2+2x3,⋯,2+2xn ，下列结论正确的是（    ）
    A、平均数为20，方差为4 B、平均数为11，方差为4 C、平均数为21，方差为8 D、平均数为20，方差为8

    查看试题解析

  • 5. 学校医务室对本校高一 1000 名新生的实力情况进行跟踪调查，随机抽取了 100 名学生的体检表，得到的频率分布直方图如下，若直方图的后四组的频率成等差数列，则估计高一新生中视力在 4.8 以下的人数为（   ）

    A、600 B、390 C、610 D、510

    查看试题解析

  • 6. 如果一组数中每个数减去同一个非零常数，则这一组数的（ ）
    A、平均数不变，方差不变 B、平均数改变，方差改变 C、平均数不变，方差改变 D、平均数改变，方差不变

    查看试题解析

  • 7. 演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是（   ）
    A、中位数 B、平均数 C、方差 D、极差

    查看试题解析

  • 8. 总体由编号为01，02，…，19，20的20个个体组成，利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为（ ）
    A、08 B、07 C、01 D、02

    查看试题解析

  • 9. 如图是 2018 年我校举办“激扬青春，勇担责任”演讲比赛大赛上，七位评委为某位选手打出的分数的茎叶图，去掉一个最高分和一个最低分后，所剩数据的中位数和平均数分别为 （ ）

    A、85；87 B、84；86 C、85；86 D、84；85

    查看试题解析

  • 10. 某公司生产 A ， B ， C 三种不同型号的轿车，产量之比依次为 2:3:4 ，为检验该公司的产品质量，用分层抽样的方法抽取一个容量为 n 的样本，若样本中 A 种型号的轿车比 B 种型号的轿车少8辆，则 n= （    ）
    A、96 B、72 C、48 D、36

    查看试题解析

  • 11. 某校共有学生2000名，各年级男、女生人数如右表．已知在全校学生中随机抽取1名，抽到二年级女生的概率是0.19．现用分层抽样的方法在全校抽取64名学生，则应在三年级抽取的女学生人数为（   ）

    一年级

    二年级

    三年级

    女生

    373

    x

    y

    男生

    377

    370

    250
    A、24 B、16 C、12 D、8

    查看试题解析

  • 12. 如图，这是某校高三年级甲、乙两班在上学期的5次数学测试的班级平均分的茎叶图，则下列说法不正确的是（    ）

    A、甲班的数学成绩平均分的平均水平高于乙班 B、甲班的数学成绩的平均分比乙班稳定 C、甲班的数学成绩平均分的中位数高于乙班 D、甲、乙两班这5次数学测试的总平均分是103

    查看试题解析

  • 13. 甲、乙两人在一次射击比赛中各射靶5次,两人成绩的统计表如下表所示,则有以下四种说法：

    甲

    环数

    4

    5

    6

    7

    8

    频数

    1

    1

    1

    1

    1

    乙

    环数

    5

    6

    9

    频数

    3

    1

    1

    ①甲成绩的平均数小于乙成绩的平均数；   ②甲成绩的中位数等于乙成绩的中位数；

    ③甲成绩的方差小于乙成绩的方差；       ④甲成绩的极差小于乙成绩的极差．

    其中正确命题的个数是（    ）（注： s2=1n[(x 1−x¯  )2+(x  2−x¯ )2+⋯+(x n−x¯ )2] ，其中 x¯ 为数据 x 1, x 2, ⋯,x n 的平均数）

    A、1 B、2 C、3 D、4

    查看试题解析

  • 14. 在某次高中学科竞赛中，4000名考生的参赛成绩统计如图所示，60分以下视为不及格，若同一组中数据用该组区间中点作代表，则下列说法中有误的是（    ）

    A、成绩在 [70 ， 80] 分的考生人数最多 B、不及格的考生人数为1000人 C、考生竞赛成绩的平均分约70.5分 D、考生竞赛成绩的中位数为75分

    查看试题解析

二、填空题

  • 15. 若数据 2,x,2,2 的方差为 0 ，则 x= ．

    查看试题解析

  • 16. 一学校高中部有学生2 000人，其中高一学生800人，高二学生600人，高三学生600人.现采用分层抽样的方法抽取容量为50的样本，那么高一、高二、高三各年级被抽取的学生人数分别为 ．

    查看试题解析

  • 17. 2020年年初，新冠肺炎疫情袭击全国.口罩成为重要的抗疫物资，为了确保口罩供应，某工厂口罩生产线高速运转，工人加班加点生产.设该工厂连续5天生产的口罩数依次为 x1 ， x2 ， x3 ， x4 ， x5 （单位：十万只），若这组数据 x1 ， x2 ， x3 ， x4 ， x5 的方差为1.44，且 x12 ， x22 ， x32 ， x42 ， x52 的平均数为4，则该工厂这5天平均每天生产口罩十万只.

    查看试题解析

  • 18. 为了了解某地高一学生的体能状况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图(如图)，则 x= ， 估计该地学生跳绳次数的中位数是.

    查看试题解析

三、解答题

  • 19. 从某市主办的科技知识竞赛的学生成绩中随机选取了40名学生的成绩作为样本，已知这些成绩全部在40分至100分之间，现将成绩按如下方式分成6组：第一组 [40 ， 50) ；第二组 [50 ， 60) ； … ；第六组 [90 ， 100] ，并据此绘制了如图所示的频率分布直方图．

    (1)、求成绩在区间 [80 ， 90) 内的学生人数；
    (2)、估计这40名学生成绩的众数和中位数．

    查看试题解析

  • 20. 为了了解高一学生的体能情况，某校抽取部分高一学生进行一分钟跳绳次数测试，将所得数据整理后分成 7 组：第一组 [70 ， 80) ，第二组 [80 ， 90) ，第三组 [90 ， 100) ，第四组 [100 ， 110) ，第五组 [110 ， 120) ，第六组 [120 ， 130) ，第七组 [130 ， 140] ，得到如图所示的频率分布直方图（不完整）.

    (1)、求第四组的频率并补全频率分布直方图；
    (2)、现采取分层抽样的方法从第三、四、五组中随机抽取 6 名学生测量肺活量，求每组抽取的学生数.

    查看试题解析

  • 21. 为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A，B两组，每组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液，每只小鼠给服的溶液体积相同、摩尔浓度相同。经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图：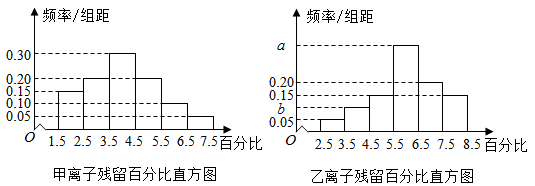


    记C为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P（C）的估计值为0.70.

    (1)、求乙离子残留百分比直方图中a，b的值；
    (2)、分别估计甲，乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）

    查看试题解析

  • 22. 某科研课题组通过一款手机APP软件，调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”)，得到如下的频数分布表

    周跑量(km/周)

    [10，15 )

    [15，20 )

    [20，25 )

    [25，30 )

    [30，35 )

    [35，40 )

    [40，45 )

    [45，50 )

    [50，55 )

    人数

    100

    120

    130

    180

    220

    150

    60

    30

    10
    (1)、在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图：


    注：请先用铅笔画，确定后再用黑色水笔描黑

    (2)、根据以上图表数据计算得样本的平均数为28.5km，试求样本的中位数(保留一位小数)，并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
    (3)、根据跑步爱好者的周跑量，将跑步爱好者分成以下三类，不同类别的跑者购买的装备的价格不一样，如下表：

    周跑量

    小于20公里

    20公里到40公里

    不小于40公里

    类别

    休闲跑者

    核心跑者

    精英跑者

    装备价格（单位：元）

    2500

    4000

    4500

    根据以上数据，估计该市每位跑步爱好者购买装备，平均需要花费多少元?

    查看试题解析