2016年湖北省孝感市安陆市中考数学模拟试卷（3月份）

试卷更新日期：2016-04-26 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\frac{1}{2}$ 的相反数是（　　）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 雾霾天气影响着我国北方中东部地区，给人们的健康带来严重的危害．为了让人们对雾霾有所了解．摄影师张超通过显微镜，将空气中细小的霾颗粒放大1000倍，发现这些霾颗粒平均直径为10微米〜20微米，其中20微米（1米=1000000微米）用科学记数法可表示为（　　）

A、2×10⁵米 B、0.2×10^﹣4米 C、2×10^﹣5米 D、2×10^﹣4米

查看试题解析
3.
直线a、b、c、d的位置如图，如果∠1=100°，∠2=100°，∠3=125°，那么∠4等于（　　）

A、80° B、65° C、60° D、55°

查看试题解析
4. 下列运算正确的是（　　）

A、a+2a=2 $a^{2}$ B、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ C、 ${(x - 3)}^{2}$ = $x^{2}$ ﹣9 D、 ${(x^{2})}^{3} = x^{6}$

查看试题解析
5.
如图所示，反映的是九（1）班学生外出乘车、步行、骑车的人数直方图的一部分和圆形分布图，下列说法①①九（1）班外出步行有8人；②在圆形统计图中，步行人数所占的圆心角度数为82°；③九（1）班外出的学生共有40人；④若该校九年级外出的学生共有500人，那么估计全年级外出骑车的人约有150人，其中正确的结论是（　　）

A、①②③ B、①③④ C、②③ D、②④

查看试题解析
6. 在平面直角坐标系中，已知点A（﹣4，2），B（﹣6，﹣4），以原点O为位似中心，相似比为 $\frac{1}{2}$ ，把△ABO缩小，则点A的对应点A′的坐标是（　　）

A、（﹣2，1） B、（﹣8，4） C、（﹣8，4）或（8，﹣4） D、（﹣2，1）或（2，﹣1）

查看试题解析
7. 若规定sin（α﹣β）=sinαcosβ﹣cosαsinβ，则sin15°=（　　）

A、 $\frac{\sqrt{2} - 1}{2}$ B、 $\frac{\sqrt{2} - \sqrt{6}}{4}$ C、 $\frac{\sqrt{3} - 1}{2}$ D、 $\frac{\sqrt{6} - \sqrt{2}}{4}$

查看试题解析
8.
如图，在平面直角坐标系中，矩形ABOC的两边在坐标轴上，OB=1，点A在函数y=﹣ $\frac{2}{x}$ （x＜0）的图象上，将此矩形向右平移3个单位长度到A₁B₁O₁C₁的位置，此时点A₁在函数y= $\frac{k}{x}$ （x＞0）的图象上，C₁O₁与此图象交于点P，则点P的纵坐标是（　　）

A、 $\frac{5}{3}$ B、 $\frac{3}{4}$ C、 $\frac{4}{3}$ D、 $\frac{2}{3}$

查看试题解析
9. 《九章算术》商功章有题：一圆柱形谷仓，高1丈3尺3 $\frac{1}{3}$ 寸，容纳米2000斛（1丈=10尺，1尺=10寸，斛为容积单位，1斛≈1.62立方尺，π=3），则圆柱底周长约为（注：圆柱体的体积=底面积×高）（　　）

A、1丈3尺 B、5丈4尺 C、9丈2尺 D、48丈6尺

查看试题解析
10.
已知二次函数y=ax²+bx+c的图象如图所示，记m=|a﹣b+c|+|2a+b+c|，n=|a+b+c|+|2a﹣b﹣c|．则下列选项正确的是（　　）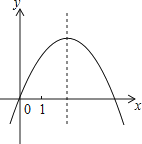

A、m＜n B、m＞n C、m=n D、m、n的大小关系不能确定

查看试题解析

二、填空题

11. 式子 $\sqrt{2 - x}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 已知a²﹣b²= $\sqrt{6}$ ，a﹣b= $\sqrt{3}$ ，则a+b= ．

查看试题解析
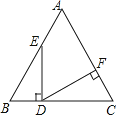
13.
如图，在等边△ABC中，点D为BC边上的点，DE⊥BC交AB于E，DF⊥AC于F，则∠EDF的度数为．

查看试题解析
14.
如图，直线y=﹣ $\frac{4}{3}$ x+4与x轴、y轴分别交于A、B两点，把△AOB绕点A顺时针旋转90°后得到△AO′B′，则点B′的坐标是．

查看试题解析
15.
如图，矩形ABCD中，AB=8，BC=4，点E在边AB上，点F在边CD上，点G、H在对角线AC上，若四边形EGFH是菱形，则AE的长是．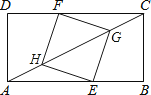

查看试题解析
16. 观察下列等式
1²=1= $\frac{1}{6}$ ×1×2×（2+1）
1²+2²= $\frac{1}{6}$ ×2×3×（4+1）
1²+2²+3²= $\frac{1}{6}$ ×3×4×（6+1）
1²+2²+3²+4²= $\frac{1}{6}$ ×4×5×（8+1）…
可以推测1²+2²+3²+…+n²= ．

查看试题解析

三、解答题

17.
解不等式 $\frac{1}{2}$ x﹣ $\frac{2}{3}$ ≥ $\frac{2}{3}$ x﹣ $\frac{1}{3}$ ，并把它的解集在数轴上表示出来

查看试题解析
18.
如图，已知在△ABC中，∠A=90°

(1)、请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作图痕迹，不写作法和证明）．

(2)、若∠B=60°，AB=3，求⊙P的面积．

查看试题解析
19.
感知：如图①，点E在正方形ABCD的边BC上，BF⊥AE于点F，DG⊥AE于点G，可知△ADG≌△BAF．（不要求证明）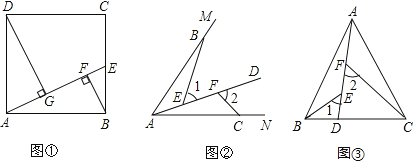

(1)、拓展：如图②，点B、C分别在∠MAN的边AM、AN上，点E、F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2= ∠ BAC，求证：△ABE≌△CAF．

(2)、应用：如图③，在等腰三角形ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为9，则△ABE与△CDF的面积之和为．

查看试题解析
20. 某校为了选拔学生参加“汉字听写大赛”，对九年级一班、二班各10名学生进行汉字听写测试．计分采用10分制（得分均取整数），成绩达到6分或6分以上为及格，得到9分为优秀，成绩如表1所示，并制作了成绩分析表（表2）．
表1
一班
5
8
8
9
8
10
10
8
5
5
二班
10
6
6
9
10
4
5
7
10
8
表2
班级
平均数
中位数
众数
方差
及格率
优秀率
一班
7.6
8
a
3.82
70%
30%
二班
b
7.5
10
4.94
80%
40%

(1)、在表2中，a= ， b=；

(2)、有人说二班的及格率、优秀率均高于一班，所以二班比一班好；但也有人认为一班成绩比二班好，请你给出坚持一班成绩好的两条理由；

(3)、一班、二班获满分的中同学性别分别是1男1女、2男1女，现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”，用树状图或列表法求出恰好抽到1男1女两位同学的概率．

查看试题解析
21. 已知：二次函数y=x²﹣3（m﹣1）x+3m﹣4（m为实数）的图象与x轴交于A（x₁ ， 0）、B（x₂ ， 0）（x₁≠x₂）两点．

(1)、求m的取值范围；

(2)、若 $\frac{1}{O A} + \frac{1}{O B} = \frac{2}{O A} • \frac{1}{O B}$ （O为坐标原点），求m的值．

查看试题解析
22.
如图，已知AB为⊙O直径，AC是⊙O的弦，∠BAC的平分线AD交⊙O于D，过点D作DE⊥AC交AC的延长线于点E，OE交AD于点F，cos∠BAC=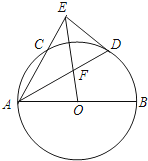 $\frac{3}{5}$

(1)、求证：DE是⊙O的切线；

(2)、
若AF=8，求DF的长．

查看试题解析
23.
市一中准备组织学生及学生家长到武汉大学参观体验，为了便于管理，所有人员到武汉必须乘坐在同一列动车上；根据报名人数，若都买一等座单程火车票需2556元，若都买二等座单程火车票且花钱最少，则需1530元；已知学生家长与教师的人数之比为2：1，安陆到武汉的动车票价格（动车学生票只有二等座可以打6折）如下表所示：

(1)、参加参观体验的老师、家长与学生各有多少人？

(2)、由于各种原因，二等座火车票单程只能买x张（x小于参加参观体验的人数），其余的须买一等座火车票，在保证每位参与人员都有座位坐的前提下，请你设计最经济的购票方案，并写出购买火车票的总费用（单程）y与x之间的函数关系式．

(3)、请你做一个预算，按第（2）小题中的购票方案，购买单程火车票的总费用至少是多少钱？最多是多少钱？

查看试题解析
24.
抛物线y=ax²+bx+c（a≠0）与x轴交于A（2，0），B（4，0）两点，与y轴交于点C（0，2）．

(1)、求抛物线的解析式；

(2)、点P从点O出发，乙每秒2个单位长度的速度向点B运动，同时点E也从点O出发，以每秒1个单位长度的速度向点C运动，设点P的运动时间t秒（0＜t＜2）．
①过点E作x轴的平行线，与BC相交于点D（如图所示），当t为何值时， $\frac{1}{O P} + \frac{1}{D E}$ 的值最小，求出这个最小值并写出此时点E、P的坐标；
②在满足①的条件下，抛物线的对称轴上是否存在点F，使△EFP为直角三角形？若存在，请直接写出点F的坐标；若不存在，请说明理由．

查看试题解析

班级	平均数	中位数	众数	方差	及格率	优秀率
一班	7.6	8	a	3.82	70%	30%
二班	b	7.5	10	4.94	80%	40%