江苏省兴化市2020年中考数学一模试卷
试卷更新日期：2020-05-20 类型：中考模拟
一、选择题（本大题共有6小题，每小题3分，共18分）
-
1. -4的倒数是（ ）A、4 B、-4 C、 D、2. “厉害了，我的国！”2020年2月28日，国家统计局对外公布，2019年我国国内生产总值（GDP）首次站上99000 000 000 000元的历史新台阶，把99000 000 000 000用科学记数法表示为（ ）A、9.9×1013 B、9.9×1012 C、9.9×1011 D、9.9×1093. 下列几何体中，主视图是等腰三角形的是（ ）A、
B、
C、
D、
4. 关于x的一元二次方程x2-4x+1=0的根的情况是（ ）A、有两相等实数根 B、有两不相等实数根 C、无实数根 D、不能确定5. 如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则∠3的度数等于（ ）
A、20° B、30° C、50° D、80°6. 已知实数a，b满足a+b=2，ab= ，则a-b的结果是（ ）A、1 B、- C、±1 D、±二、填空题
-
7. 二次根式 中的x的取值范围是。8. 单项式5mn2的次数为。9. 已知一个正n边形的内角和为1080°，则n=。10. 数据1,2,3,4,5的方差是 ．11. 将抛物线y=-x2先向下平移2个单位，再向右平移3个单位后所得抛物线的解析式为。12. 因式分解：a2b-4ab+4b= ．13. 如图，在△ABC中，∠ABC=90°，∠C=20°，DE是边AC的垂直平分线，连结AE，则∠BAE等于°。
14. 已知一个圆锥形零件的母线长为13cm，底面半径为5cm，则这个圆锥形的零件的侧面积为cm²。（结果用π表示）。15. 设m、n是方程x2+x-2021=0的两个实数根，则m²+2m+n的值为。
16. 如图，扇形AOB，且OB=4，∠AOB=90°，C为弧AB上任意一点，过C点作CD⊥OB于点D，设△ODC的内心为E，连接OE、CE，当点C从点B运动到点A时，内心E所经过的路径长为 。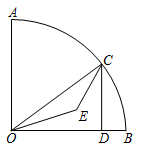
三、解答题
-
17.(1)、计算：(2)、解方程：18. 为了解朝阳社区20-60岁居民最喜欢的支付方式，某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查（每人只能选择其中一项），并将调查数据整理后绘成如下两幅不完整的统计图。请根据图中信息解答下列问题：
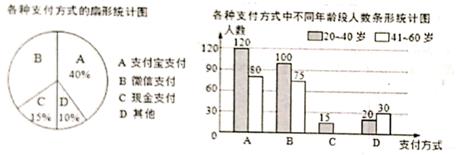(1)、求参与问卷调查的总人数。(2)、补全条形统计图。(3)、该社区中20~60岁的居民约8000人，估算这些人中最喜欢微信支付方式的人数。19. 桌面上有四张正面分别标有数字1，2，3，4的不透明的卡片，它们除数字不同外其余全部相同．现将它们背面朝上洗匀。(1)、随机翻开一张卡片，正面所标数字大于2的概率为；(2)、随机翻开一张卡片，从余下的三张卡片中再翻开一张，求翻开的两张卡片正面所标数字之和是偶数的概率。20. 已知：如图， ABCD中，AB=5，BC=3。
(1)、作∠DAB的角平分线，交CD于点E（用直尺和圈规作图，不写作法，保留作图痕迹）；(2)、求CE的长。21. 兴化市特产大闸蟹，2017年的销售额是50亿元，因优质生态，销售额是逐年增加，2019年的销售额达98亿元，若2018、2019年每年销售额增加的百分率都相同。(1)、求平均每年销售额增加的百分率；(2)、兴化市这3年大闸蟹的总销售额是多少亿元？22. 如图，A，B是两座现代化城市，C是一个古城遗址，C城在A城的北偏东30°，在B城的北偏西45°，B城在A城的正东方向，且C城与A城相距120千米，现在A、B两城市修建一条笔直的高速公路。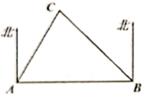
(1)、请你计算公路AB的长度（结果保留根号）；(2)、若以C为圆心，以60千米为半径的圆形区域内为古迹和地下文物保护区，请你分析公路AB会不会穿越这个保护区，并说明理由。23. 如图，一次函数y1=kx+b（k≠0）的图象与反比例函数y2= （m≠0，x<0）的图象交于点A（-3，1）和点C（-1，3），与y轴交于点B。
(1)、求一次函数与反比例函数的解析式；(2)、求△AOB的面积。24. 如图，△ABC为等腰三角形，AB=AC，O是底边BC的中点，⊙O与腰AB相切于点D。
(1)、求证：AC与⊙O相切；(2)、已知AB=5，BC=6，求⊙O的半径。25. 如图，在矩形ABCD中，已知AB=2 ，AD=2，点P是对角线BD上一动点（不与B，D重合），连接AP，过点P作PE⊥AP，交DC于点E，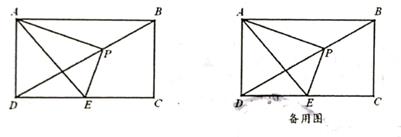
(1)、求证：∠PAD=∠PEC；(2)、当点P是BD的中点时，求DE的值；(3)、在点P运动过程中，当DE= 时，求BP的值。26. 已知，抛物线y=ax²-2amx+am2+2m-5与x轴交于A（x1 ， 0），B（x2 ， 0）（x1<x2）两点，顶点为P。(1)、当a=1，m=2时，求线段AB的长度；(2)、当a=2，若点P到x轴的距离与点P到y轴的距离相等，求该抛物线的解析式；(3)、若a= ，当2m-5≤x≤2m-2时，y的最大值为2，求m的值。