广东省深圳2020年中考数学二模试卷
试卷更新日期:2020-05-20 类型:中考模拟
一、选择题
-
1. -3的绝对值为( )A、3 B、-3 C、±3 D、92. 一条数学信息在一周内被转发了2 180 000次,将数据2 180 000用科学记数法表示为( )A、2.18106 B、2.18x105 C、21.8x106 D、21.8x1053. 下列图形既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图是由一些小立方体与圆锥组合成的立体图形,它的主视图是( )
4. 如图是由一些小立方体与圆锥组合成的立体图形,它的主视图是( )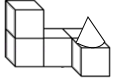 A、
A、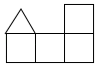 B、
B、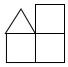 C、
C、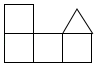 D、
D、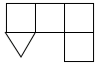 5. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如表:
5. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如表:投中次数
3
5
6
7
8
人数
1
3
2
2
2
则这些队员投中次数的众数、中位数和平均数分别为( )
A、5,6,6 B、2,6,6 C、5,5,6 D、5,6,56. 下列计算正确的是( )A、a2+a3=a5 B、a8÷a4=a4 C、(-2ab)2=-4a2b2 D、(a+b)2=a2+b27. 如图,直线l1∥l2 , 直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是( ) A、65° B、55° C、45° D、35°8. 下列命题中正确的是( )A、函数y= 的自变量x的取值范围是x>3 B、菱形是中心对称图形,但不是轴对称图形 C、一组对边平行,另一组对边相等四边形是平行四边形 D、三角形的外心到三角形的三个顶点的距离相等9. 如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
A、65° B、55° C、45° D、35°8. 下列命题中正确的是( )A、函数y= 的自变量x的取值范围是x>3 B、菱形是中心对称图形,但不是轴对称图形 C、一组对边平行,另一组对边相等四边形是平行四边形 D、三角形的外心到三角形的三个顶点的距离相等9. 如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
作法:
①以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E:
②分别以D,E为画心,大于 DE的长为半径画弧,两弧在∠AOB内交于一点c:
③画射线OC,射线OC就是∠AOB的角平分线
A、ASA B、SAS C、SSS D、AAS10. 在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重合,顶点A,B恰好分制落在函数y=- (x<0),y= (x>0)的图象上,则sin∠ABO的值为( ) A、 B、 C、 D、11. 如图,抛物线y= (x+2)(x-8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D。下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切其中正确结论的个数是( )
A、 B、 C、 D、11. 如图,抛物线y= (x+2)(x-8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D。下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切其中正确结论的个数是( )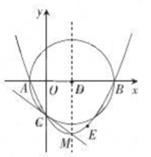 A、1 B、2 C、3 D、412. 如图,菱形ABCD中,AB=AC,点E,F分别为边AB,BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE·AD=AH·AF;其中结论正确的个数是( )
A、1 B、2 C、3 D、412. 如图,菱形ABCD中,AB=AC,点E,F分别为边AB,BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE·AD=AH·AF;其中结论正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 多项式x2+mx+25能用完全平方公式分解因式,则m= .14. 小强同学从-1,0,1,2,3,4这六个数中任选一个数,满足不等式x+1<2的概率是。15. 定义一种新运算:a b=b2-ab,如:1 2=22-1×2=2,则(-1 2) 3=。16. 如图,矩形OABC的边AB与x轴交于点D,与反比例函数y= (k>0)在第一象限的图象交于点E,∠AOD=30°,点E的纵坐标为1,△ODE的面积 ,k的值是。

三、解答题
-
17. 计算:20190-(-1)2019+ -|-3 |18. 先化简,再求值: ,其中x满足x2-2x-2=0.19. 某校为了解八年级男生“立定跳远”成绩的情况,随机选取该年级部分男生进行测试,以下是根据测试成绩绘制的统计图表的一部分。
成绩
频数(人)
频率
优秀
15
0.3
良好
及格
不及格
5

根据以上信息,解答下列问题
(1)、被测试男生中,成绩等级为“优秀”的男生人数为人,成绩等级为“及格”以上的男生人数占被测试男生总人数的百分比为%;(2)、被测试男生的总人数为人,成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为%;(3)、若该校八年级共有180名男生,根据调查结果,估计该校八年级男生成绩等级为“良好”的学生人数。20. 某车行去年A型车的销售总额为6万元,今年每辆车的售价比去年减少400元,若卖出的数量相同,销售总额将比去年减少20%,(1)、求今年A型车每辆车的售价。(2)、车行计划新进一批A型车和B型车共45辆,已知A、B型车的进货价格分别是1100元,1400元,今年B型车的销售价格是2000元,要求B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获得最大利润,最大利润是多少?21. 在一次海上救援中,两艘专业救助船A,B同时收到某事故渔船的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里。 (1)、求收到求救讯息时事故渔船P与救助船B之间的距离;(2)、若救助A,B分别以40海里/小时,30海里/小时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达。22. 如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)、求收到求救讯息时事故渔船P与救助船B之间的距离;(2)、若救助A,B分别以40海里/小时,30海里/小时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达。22. 如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.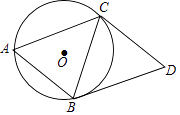 (1)、求证:BD是⊙O的切线;
(1)、求证:BD是⊙O的切线;
(2)、若AB=10,cos∠BAC= ,求BD的长及⊙O的半径.23. 如图,抛物线y=ax2+bx+4交x轴于A(-3,0),B(4,0)两点,与y轴交于点C,连接AC,BC。
点P是第一象限内抛物线上的一个动点,点P的横坐标为m。
(1)、求此抛物线的表达式;(2)、过点P作PM⊥x轴,垂足为点M,PM交BC于点Q,试探究点P在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形。若存在,请求出此时点Q的坐标,若不存在,请说明理由;(3)、过点P作PN⊥BC,垂足为点N,请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?