安徽省安庆市2020年中考数学模拟试卷
试卷更新日期:2020-05-20 类型:中考模拟
一、选择题
-
1. -2020的相反数是( )A、2020 B、-2020 C、 D、2. 大数据显示,2019年9月30日至10月6日,与新中国成立70周年阅兵相关信息全网传播总量约1.3亿条. 用科学记数法表示1.3亿为( )A、1.3×107 B、1.3×108 C、0.13×109 D、13×1073. 下列运算正确的是( )A、a4+a2=a6 B、4a2-2a2=2a2 C、(a4)2=a6 D、a4•a2=a84. 如图所示的零件,其主视图正确的是( )
 A、
A、 B、
B、 C、
C、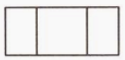 D、
D、 5. 为了调查某校学生课后参加体育锻炼的时间,学校体育组随机抽样调查了若干名学生的每天锻炼时间,统计如下表:
5. 为了调查某校学生课后参加体育锻炼的时间,学校体育组随机抽样调查了若干名学生的每天锻炼时间,统计如下表:每天锻炼时间(分钟)
20
40
60
90
学生数(人)
2
3
4
1
下列说法错误的是( )
A、众数是60分钟 B、平均数是52.5分钟 C、样本容量是10 D、中位数是50分钟6. 已知在平面直角坐标系中,P(1,a)是一次函数y=-2x+1的图像与反比例函数 图像的交点,则实数k的值为( )A、-1 B、1 C、2 D、37. 某企业今年1月份产值为a万元,2月份比1月份减少了15%,3月份比2月份增加了5%,则3月份的产值为( )A、(a+15%)(a-5%)万元 B、(a-15%)(a+5%)万元 C、a(1+15%)(1-5%)万元 D、a(1-15%)(1+5%)万元8. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知∠A=90°,BD=3,BC=13,则正方形ADOF的面积是( )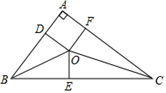 A、6 B、5 C、4 D、39. 对x , y定义一种新运算,规定: (其中a , b均为非零常数),这里等式右边是通常的四则运算,例如: .已知:T(0,1)=3, ,若m满足不等式组 ,则整数m的值为( )A、-2和-1 B、-1和0 C、0和1 D、1和210. 如图,在边长为 的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P , 则线段CP的最小值为( )
A、6 B、5 C、4 D、39. 对x , y定义一种新运算,规定: (其中a , b均为非零常数),这里等式右边是通常的四则运算,例如: .已知:T(0,1)=3, ,若m满足不等式组 ,则整数m的值为( )A、-2和-1 B、-1和0 C、0和1 D、1和210. 如图,在边长为 的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P , 则线段CP的最小值为( )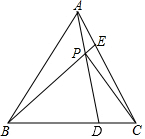 A、1 B、2 C、 D、
A、1 B、2 C、 D、二、填空题
-
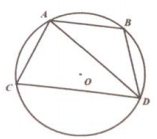
11. 因式分解:3a2-27=12. 如图,点A、B、C、D在⊙O上,满足AB//CD , 且AB=AC , 若∠B=110°,则∠DAC的度数为
 13. 如图,矩形ABCD中,AB=4,AD=8,点E为AD上一点,将△ABE沿BE折叠得到△FBE , 点G为CD上一点,将△DEG沿EG折叠得到△HEG , 且E、F、H三点共线,当△CGH为直角三角形时,AE的长为
13. 如图,矩形ABCD中,AB=4,AD=8,点E为AD上一点,将△ABE沿BE折叠得到△FBE , 点G为CD上一点,将△DEG沿EG折叠得到△HEG , 且E、F、H三点共线,当△CGH为直角三角形时,AE的长为
三、解答题
-
14. 计算:15. 中国古代数学著作《孙子算经》中有这样一个问题,原文:今有三人共车,二车空;二人共车,九人步,人与车各几何?译文为:今有若干人乘车,每3人共乘一车,所乘车都坐满,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?16. 如图,在平面直角坐标系中,给出了格点△ABC(顶点是网格线的交点),已知点B的坐标为(1,2).
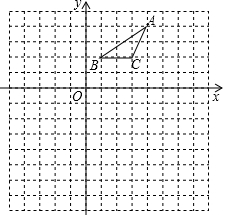 (1)、画出△ABC关于y轴对称的△A1B1C1 , 并写出点B1的坐标;(2)、在给定的网格中,以点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2 , 画出△A2B2C2;并写出点B2的坐标.17. 有下列等式:
(1)、画出△ABC关于y轴对称的△A1B1C1 , 并写出点B1的坐标;(2)、在给定的网格中,以点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2 , 画出△A2B2C2;并写出点B2的坐标.17. 有下列等式:第1个等式: ; 第2个等式, ;第3个等式: ; 第4个等式: ;…
请你按照上面的规律解答下列问题:
(1)、第5个等式是;(2)、写出你猜想的第n个等式;(用含n的等式表示),并证明其正确性.18. 为倡导“绿色出行,低碳生活”的号召,今年春天,安庆市的街头出现了一道道绿色的风景线--“共享单车”. 图(1)所示的是一辆共享单车的实物图. 图(2)是这辆共享单车的部分几何示意图,其中车架档AC长为40cm,座杆CE的长为18cm. 点A、C、E在同一条直线上,且∠CAB=60°,∠ACB=75°
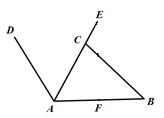 (1)、求车座点E到车架档AB的距离;(2)、求车架档AB的长.19. 如图,⊙O为△ABC的外接圆,直线MN与⊙O相切于点C , 弦BD∥MN , AC与BD相交于点E.
(1)、求车座点E到车架档AB的距离;(2)、求车架档AB的长.19. 如图,⊙O为△ABC的外接圆,直线MN与⊙O相切于点C , 弦BD∥MN , AC与BD相交于点E.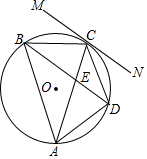 (1)、求证:∠CAB=∠CBD;(2)、若BC=5,BD =8,求⊙O的半径.20. 受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动。为了解学生上网课使用的设备类型,某校从“电脑、手机、电视、其它"四种类型的设备对学生做了一次抽样调查。调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)、求证:∠CAB=∠CBD;(2)、若BC=5,BD =8,求⊙O的半径.20. 受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动。为了解学生上网课使用的设备类型,某校从“电脑、手机、电视、其它"四种类型的设备对学生做了一次抽样调查。调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题: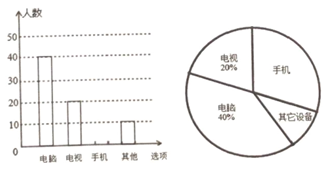 (1)、补全条形统计图;(2)、若该校共有1500名学生,估计全校用手机上网课的学生共有名;(3)、在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.21. 海鲜门市的某种海鲜食材,成本为10元/千克,每天的进货量p(千克)与销售价格x(元/千克)满足函数关系式 ,从市场反馈的信息发现,该海鲜食材每天的市场需求量q(千克)与销售价格x(元/千克)满足一次函数关系,部分数据如下表:
(1)、补全条形统计图;(2)、若该校共有1500名学生,估计全校用手机上网课的学生共有名;(3)、在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.21. 海鲜门市的某种海鲜食材,成本为10元/千克,每天的进货量p(千克)与销售价格x(元/千克)满足函数关系式 ,从市场反馈的信息发现,该海鲜食材每天的市场需求量q(千克)与销售价格x(元/千克)满足一次函数关系,部分数据如下表:销售价格x(元/千克)
10
12
…
30
市场需求量q(千克)
30
28
…
10
(已知按物价部门规定销售价格x不低于10元/千克且不高于30元/千克)
(1)、请写出q与x的函数关系式:;(2)、当每天的进货量小于或等于市场需求量时,这种海鲜食材能全部售出,而当每天的进货量大于市场需求量时,只能售出符合市场需求量的海鲜食材,剩余的海鲜食材由于保质期短而只能废弃.①求出每天获得的利润y(元)与销售价格x的函数关系式;
②为了避免浪费,每天要确保这种海鲜食材能全部售出,求销售价格为多少元时,每天获得的利润(元)最大值是多少?
22. 如图(1),已知正方形ABCD中,点E、F分别在边BC、CD上,BE=DF , AE、AF分别交BD于点G、H.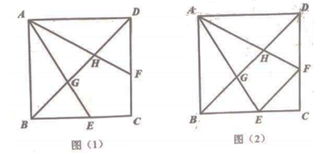 (1)、求证:BG=DH;(2)、连接FE , 如图(2),当EF=BG时.
(1)、求证:BG=DH;(2)、连接FE , 如图(2),当EF=BG时.①求证:AD•AH=AF•DF;
②直接写出 的比值.