上海市杨浦区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-05-20 类型：期末考试

进入出卷网下载

一、填空题

1. 若x³=8，则x= ．

查看试题解析
2. 1的四次方根是．

查看试题解析
3. 计算： $27^{\frac{2}{3}}$ = ．

查看试题解析
4. 用计算器比较大小：－π－．（在横线上填写“＞”、“＜”或“=”）

查看试题解析
5. 如图， $| a - b | - \sqrt{b^{2}}$ = ．

查看试题解析
6. 计算： $\sqrt{6} \times 2 \sqrt{3}$ = ．

查看试题解析
7. 上海迪士尼乐园是中国大陆首座迪士尼乐园，2016年6月16日开园，其总面积约为 $3.90 \times 10^{8}$ 平方米，这个近似数有个有效数字．

查看试题解析
8. 在平面直角坐标系中，点A（2，1）关于x轴对称的点的坐标是.

查看试题解析
9. 在平面直角坐标系中，经过点Q（1，-5）且垂直于y轴的直线可以表示为直线．

查看试题解析
10. 如图，直线AB，CD相交于点O，OE平分∠BOC，已知∠COE＝65°，则∠BOD＝°.

查看试题解析
11. 如图，直线a、b被直线c所载，a//b，已知 $∠ 1 = 60 °$ ，则 $∠ 2$ = ︒

查看试题解析
12. 如图，如果∠＝∠ ，那么根据可得AD∥BC.(写出一个正确的就可以)

查看试题解析
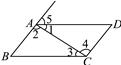13. 如图，已知在 $Δ A B C$ 中，AB=AC，点D在边BC上，要使BD=CD，还需添加一个条件，这个条件是．（只需填上一个正确的条件）

查看试题解析
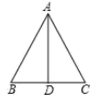14. 在△ABC中，AB=AC，把△ABC折叠，使点B与点A重合，折痕交AB于点M，交BC于点N．如果△CAN是等腰三角形，则∠B的度数为．

查看试题解析

二、单选题

15. 在0、 $- 2 、 \sqrt{2} 、 \sqrt[3]{4} 、 3.1416 、 0. \overset{\cdot}{2} \overset{\cdot}{3} 、 \frac{22}{7} 、 π 、 8 \frac{1}{3} 、 0.3737737773 \dots$ （它的位数无限且相邻两个“3”之间“7”的个数依次加1个），这十个数中，无理数的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
16. 下列运算中，正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 ${(\sqrt{3} - \sqrt{2})}^{2} = 1$ C、 $\sqrt{{(- 2)}^{2} \times 5} = - 2 \sqrt{5}$ D、 $\sqrt{(- 3) \times (- 5)} = \sqrt{3} \times \sqrt{5}$

查看试题解析
17. 如图，在 $Δ A B C$ 中， $∠ B A C = 90 °$ ，且 $A D ⊥ B C$ 于点D， $∠ B = 35 °$ ，那么下列说法中不正确的是（）

A、直线AB与直线BC的夹角为 $35 °$ B、直线AC与直线AD的夹角为 $55 °$ C、点C到直线AD的距离是线段CD的长 D、点B到直线AC的距离是线段AB的长

查看试题解析
18. 下列说法中，正确的有（）
①如果两条直线被第三条直线所载，那么内错角相等；②经过直线外的一点，有且只有一条直线与已知直线平行；③联结直线外一点与直线上各点的所有线段中，垂线段最短；④如果两个角相等，那么这两个角是对顶角．

A、0个 B、1个 C、2个 D、3个

查看试题解析
19. 下列长度的三根木棒，不能构成三角形框架的是（）

A、7cm，10cm，4cm B、5cm，7cm，11cm C、5cm，7cm，10cm D、5cm，10cm，15cm

查看试题解析
20. 在如图的方格纸中，每个小方格都是边长为1的正方形，点A、B是方格纸中的两个格点（即正方形的顶点），在这个5×5的方格纸中，找出格点C使△ABC的面积为2个平方单位，则满足条件的格点C的个数是（）

A、5 B、4 C、3 D、2

查看试题解析

三、综合题

21. 计算： $\sqrt[3]{- 2 + \frac{3}{64}} + \sqrt{13^{2} - 12^{2}} - \sqrt[3]{{(- 8)}^{2}}$ ；

查看试题解析
22. 计算： $(3 - 2 \sqrt{3}) \div \sqrt{3} + 3^{\frac{3}{2}} - {(\sqrt{5} + 2)}^{0}$ ；

查看试题解析
23. 利用幂的运算性质计算： $3 \sqrt{2} \times \sqrt[3]{2} \times \sqrt[6]{2}$ ．

查看试题解析
24. 如图，点A、B、C和点D、E、F分别在同一直线上， $∠ A = ∠ F$ ， $∠ C = ∠ D$ ，试说明 $∠ α 与 ∠ β$ 相等的理由．
解：因为 $∠ A = ∠ F$ （已知）

所以DF//AC（）

所以 $∠ D = ∠ D B A$ （）

又因为 $∠ C = ∠ D$ （已知），所以 $∠ C = ∠ D B A$ ．

所以// ；

所以 $∠ α =$ ∠；

又 $∠ β =$ ∠；所以 $∠ α = ∠ β$ ．

查看试题解析
25. 如图，在 $Δ A B C 和 Δ A' B' C'$ 中，已知 $∠ A = ∠ A'$ ， $∠ B = ∠ B'$ ， $A B = A' B'$ ，试把下面运用“叠合法”说明 $Δ A B C$ 和 $Δ A' B' C'$ 全等的过程补充完整：

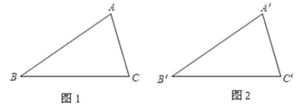
说理过程：把 $Δ A B C$ 放到 $Δ A' B' C'$ 上，使点A与点 $A'$ 重合，因为，所以可以使，并使点C和 $C'$ 在AB（ $A' B'$ ）同一侧，这时点A与 $A'$ 重合，点B与 $B'$ 重合，由于，因此，；

由于，因此，；于是点C（射线AC与BC的交点）与点 $C'$ （射线 $A' C'$ 与 $B' C'$ 的交点）重合，这样．

查看试题解析
26. 如图，在 $Δ A B C$ 中，按以下步骤作图：
①以点B为圆心，以大于 $\frac{1}{2} B C$ 的长为半径作弧，以点C为圆心，同样长为半径作弧，两弧分别相交于点M、N；

②作直线MN分别交AB、BC于点D、E，连接CD．

则直线MN和BC的关系是．若CD=CA， $∠ A = 50 °$ ，求 $∠ A C B$ 的度数．

查看试题解析
27. 如图，AC与BD相交于E，且AC=BD．

(1)、请添加一个条件能说明BC=AD，这个条件可以是：；

(2)、请你选择（1）中你所添加的一个条件，说明BC=AD的理由．

查看试题解析
28. 已知：如图，在 $Δ A B C$ 中，AC=BC，点D在AB边上，DE//AC交BC边于点E， $D F ⊥ A B$ ，垂足是D，交直线BC于点F，试说明 $Δ D E F$ 是等腰三角形的理由．

查看试题解析
29. 如图，在直角坐标平面内，已知点A的坐标（-5，0）．

(1)、写出图中B点的坐标；

(2)、若点B关于原点对称的点是C，则 $Δ A B C$ 的面积是；

(3)、在平面直角坐标系中找一点D，使 $Δ O B D$ 为等腰直角三角形，且以OB为直角边，则点D的坐标是．

查看试题解析
30. 在△ABC中，∠C=90°，∠BAC=60°，△ABC绕点C顺时针旋转，旋转角为α（0°＜α＜180°），点A、B的对应点分别是点D、E．

(1)、如图1，当点D恰好落在边AB上时，试判断DE与AC的位置关系，并说明理由．

(2)、如图2，当点B、D、E三点恰好在一直线上时，旋转角α=°，此时直线CE与AB的位置关系是．

(3)、在（2）的条件下，联结AE，设△BDC的面积S₁ ， △AEC的面积S₂ ，则S₁与S₂的数量关系是．

(4)、如图3，当点B、D、E三点不在一直线上时，（3）中的S₁与S₂的数量关系仍然成立吗？试说明理由．

查看试题解析