上海市普陀区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-05-20 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $- 1$ 、 $\sqrt{3}$ 、 $64^{\frac{1}{3}}$ 、 $0. \dot{2} \dot{1}$ 、 $\sqrt[3]{9}$ 、 $\frac{20}{7}$ 、π、 $- 0.1616616661 \dots$ （它们的位数无限，相邻两个“1”之间“6”的个数依次增加 1 个）这些数中，无理数的个数是（）

A、3 B、4 C、5 D、6

查看试题解析
2. 下列计算不正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{{(- 2)}^{2}} = 2$ C、 ${(- \sqrt{2})}^{2} = 2$ D、 $\sqrt{2^{2}} = 2$

查看试题解析
3. 如图，已知∠1 = ∠2 ，∠3 = 65° ，那么∠4 的度数是（）

A、65° B、95° C、105° D、115°

查看试题解析
4. 如图，已知△ABC ≌△AEF ，其中 AB=AE ，∠B=∠E ．在下列结论① AC=AF ，② ∠BAF=∠B ，③ EF=BC ，④ ∠BAE=∠CAF中，正确的个数有（）

A、1个 B、2 个 C、3 个 D、4 个

查看试题解析
5. 如果点A（a，b）在第二象限，那么a、b的符号是（）

A、a>0，b>0 B、a<0 ，b>0 C、a>0，b<0 D、a<0，b<0

查看试题解析
6. 下列判定两个等腰三角形全等的方法中，正确的是（）

A、一角对应相等 B、一腰和底边对应相等 C、两腰对应相等 D、底边对应相等

查看试题解析

二、填空题

7. 化简： $\sqrt{9}$ = ．

查看试题解析
8. 计算： ${(2 - \sqrt{3})}^{2}$ = ．

查看试题解析
9. 用幂的形式来表示 $\sqrt[3]{a^{2}}$ = ．

查看试题解析
10. 2017年4月26日上海最高的地标式摩天大楼“上海中心大厦”的第118层观光厅正式对公众开放，“上海中心大厦”的建筑面积达到了433954平方米，将 433954 保留三个有效数字，并用科学记数法表示是．

查看试题解析
11. 如图， CD ∥ BE ，如果∠ABE = 120° ，那么直线AB 、CD 的夹角是度．

查看试题解析
12. 在 $Δ A B C$ 中，如果 $∠ A : ∠ B : ∠ C = 4 : 5 : 9$ ，那么 $Δ A B C$ 按角分类是三角形.

查看试题解析
13. 如图，在△ABC 和△EFD 中，已知CB =DF ，∠C=∠D ，要使△ABC ≌△EFD ，还需添加一个条件，那么这个条件可以是．（只需写出一个条件）

查看试题解析
14. 如图，△ACE ≌△DBF ，如果∠E=∠F ，AD=10 ，BC=2 ，那么线段AB的长是．

查看试题解析
15. 如果将点A（1，3）先向下平移3个单位，再向右平移2个单位后，得到点B ，那么点B的坐标是．

查看试题解析
16. 已知一个等腰三角形的三边长都是整数，如果周长是 10，那么底边长等于．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A B = A C$ ， $B D$ 平分 $∠ A B C$ ，交 $A C$ 于点 $D$ 、过点 $D$ 作 $D E ∥ A B$ ，交 $B C$ 于点 $E$ ，那么图中等腰三角形有个.

查看试题解析
18. 如图，如果将△ABC 绕点A逆时针旋转40° 得到△AB'C'，那么∠ACC'=度．

查看试题解析

三、综合题

19. 计算： ${(- 8)}^{\frac{1}{3}} - \sqrt{9 \times 16} + {(π - 1)}^{0} + {(\frac{1}{2})}^{- 1}$ ．

查看试题解析
20. 计算： $\sqrt{3} \times \sqrt[4]{27} \div \sqrt[3]{9}$ .（结果用幂的形式表示）

查看试题解析
21. 如图，已知AB∥CD，∠CDE=∠ABF，试说明DE∥BF的理由．

解：因为AB∥CD（已知），
所以∠CDE=（）．
因为∠CDE=∠ABF（已知），
得=（等量代换），
所以DE∥BF（）．

查看试题解析
22. 如图，已知∠B=∠C=90°，AE⊥ED，AB=CE，点F是AD的中点．说明EF与AD垂直的理由．

解：因为AE⊥ED（已知），

所以∠AED=90°（垂直的意义）．

因为∠AEC=∠B+∠BAE（），

即∠AED+∠DEC=∠B+∠BAE．

又因为∠B=90°（已知），

所以∠BAE=∠CED（等式性质）．

在△ABE与△ECD中，

∠B=∠C（已知），AB=EC（已知），∠BAE=∠CED，

所以△ABE≌△ECD（），

得（全等三角形的对应边相等），

所以△AED是等腰三角形．

因为（已知），

所以EF⊥AD（）．

查看试题解析
23. 已知线段a和线段AB（a＜AB）．

(1)、以AB为一边，画△ABC，使AC=a，∠A=50°，用直尺、圆规作出△ABC边BC的垂直平分线，分别与边AB、BC交于点D、E，联结CD；（不写画法，保留作图痕迹）

(2)、在（1）中，如果AB=5，AC=3，那么△ADC的周长等于．

查看试题解析
24. 在直角坐标平面内，已知点 $A$ 的坐标 $(- 5 ， 0)$ ，点 $B$ 位置如图所示，点 $C$ 与点 $B$ 关于原点对称。

(1)、在图中描出点 $A$ ；写出图中点 $B$ 的坐标：，点 $C$ 的坐标：；

(2)、画出 $Δ A B C$ 关于 $y$ 轴的对称图形 $Δ A^{'} B^{'} C^{'}$ ，并求出四边形 $A^{'} B^{'} C^{'} C$ 的面积。

查看试题解析
25. 如图，已知△ABC，分别以AB、AC为边在△ABC的外部作等边三角形ABD和等边三角形ACE联结DC、BE试说明DC=BE的理由．

查看试题解析
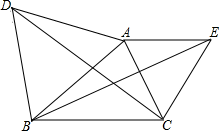26. 如图，已知△ABC中，点D、E是BC边上两点，且AD=AE，∠ BAE=∠CAD=90°，

(1)、试说明△ABE与△ACD全等的理由；

(2)、如果AD=BD，试判断△ADE的形状，并说明理由．

查看试题解析
27. 如图，在平面直角坐标系中，直线AB∥x轴，线段AB与y轴交于点M，已知点A的坐标是（－2，3），BM=4，点C与点B关于x轴对称．

(1)、在图中描出点C，并直接写出点B和点C的坐标：B ， C；

(2)、联结AC、BC，AC与x轴交于点D，试判断△ABC的形状，并直接写出点D的坐标；

(3)、在坐标平面内，x轴的下方，是否存在这样的点P，使得△ACP是等腰直角三角形？如果存在，直接写出点P的坐标；如果不存在，试说明理由．

查看试题解析