上海市奉贤区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-05-20 类型:期末考试
一、单选题
-
1. 在 , , , , , 中,有理数个数有( )A、1个 B、2个 C、3个 D、4个2. 下列运算中,正确的是( )A、 B、 C、 D、3. 如果一个三角形的三边长分别为3和7,则第三边长可能是( )A、3 B、4 C、7 D、114. 如图,用尺规作出∠AOB的角平分线OE,在作角平分线过程中,用到的三角形全等的判定方法是( )
 A、ASA B、SSS C、SAS D、AAS5. 如果两个角的两边分别平行,其中一个角是50°,则另一个角是( )A、50° B、130° C、50°或130° D、40°6. 在平面直角坐标系中,点 的坐标 ,点 的坐标 ,将线段 平移,使得 到达点 ,点 到达点 ,则点 的坐标是( )A、 B、 C、 D、
A、ASA B、SSS C、SAS D、AAS5. 如果两个角的两边分别平行,其中一个角是50°,则另一个角是( )A、50° B、130° C、50°或130° D、40°6. 在平面直角坐标系中,点 的坐标 ,点 的坐标 ,将线段 平移,使得 到达点 ,点 到达点 ,则点 的坐标是( )A、 B、 C、 D、二、填空题
-
7. 的算术平方根是 ,﹣2的相反数是 ,的绝对值是 .8. 计算 .9. 比较大小:10. 2018年末上海市常住人口总数约为24152700人,用科学记数法表示将24152700保留三个有效数字是 .11. 计算: .12. 如果点 在第四象限,则 的取值范围是 .13. 如图,在 中, , , ,则 .
 14. 如图,将一副三角板如图摆放(一块三角板的直角边与另一块三角板的斜边在同一直线上),那么 .
14. 如图,将一副三角板如图摆放(一块三角板的直角边与另一块三角板的斜边在同一直线上),那么 . 15.
15.如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: , 使△AEH≌△CEB.
 16. 等腰三角形一腰上的高与另一腰的夹角为60°,那么这个等腰三角形的底角为 .17. 在平面直角坐标系中,线段AB=5,AB∥x轴,若A点坐标为(-1,3),则B点坐标为 .18. 如图,已知 的面积为4, 平分 ,且 于点 ,那么 的面积为 .
16. 等腰三角形一腰上的高与另一腰的夹角为60°,那么这个等腰三角形的底角为 .17. 在平面直角坐标系中,线段AB=5,AB∥x轴,若A点坐标为(-1,3),则B点坐标为 .18. 如图,已知 的面积为4, 平分 ,且 于点 ,那么 的面积为 .
三、综合题
-
19. 计算:20. 计算:21. 计算(结果表示为含幂的形式):22. 如图,已知 ,根据下列要求作图并回答问题:
 (1)、作边 上的高 ;(2)、过点 作直线 的垂线,垂足为 ;(3)、点 到直线 的距离是线段的长度.
(1)、作边 上的高 ;(2)、过点 作直线 的垂线,垂足为 ;(3)、点 到直线 的距离是线段的长度.(不要求写画法,只需写出结论即可)
23. 如图,已知 , , ,试说明 的理由 24. 阅读并填空:
24. 阅读并填空:如图, 是等腰三角形, , 是边 延长线上的一点, 在边 上且联接 交 于 ,如果 ,那么 ,为什么?

解:过点 作 交 于
所以 (两直线平行,同位角相等)
()
在 与 中
所以 ,()
所以 ()
因为 (已知)
所以 ()
所以 (等量代换)
所以 ()
所以
25. 如图,在平面直角坐标系中, 为坐标原点, 的三个顶点坐标分别为 , , , 与 关于原点 对称.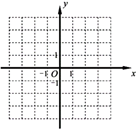 (1)、写出点 、 、 的坐标,并在右图中画出 ;(2)、求 的面积.
(1)、写出点 、 、 的坐标,并在右图中画出 ;(2)、求 的面积.