浙江省温州市平阳县、苍南县、泰顺县2020届九年级学业水平适应性考试数学试卷
试卷更新日期:2020-05-20 类型:中考模拟
一、选择题(本题有10小题,每小题4分,共40分.)
-
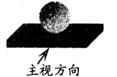
1. -5的相反数是( )A、5 B、-5 C、 D、2. 2020年春节之际,新冠肺炎疫情突如其来,危难时刻,42000多名医务工作者从全国各地驰援湖北,他们都是最美的“逆行者”,其中数据42000用科学记数法表示为( )。A、 0.42×105 B、4.2×104 C、42×103 D、4.2×1033. 由一个长方体和一个球组成的几何体如图所示,它的主视图是( )
 A、
A、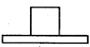 B、
B、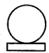 C、
C、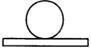 D、
D、 4. 一个不透明的袋中,装有2个黄球、3个红球和5个白球,它们除颜色外都相同.从袋中任意摸出一个球,是白球的概率是( )A、 B、 C、 D、5. 若关于x的一元二次方程4x²-4x+c=0有两个相等实数根,则c的值是( )A、-1 B、1 C、-4 D、46. 不等式组 的解是( )A、x<-1 B、x>-1 C、-1<x<4 D、x>47. 如图,梯子AC的长为2.8米,则梯子顶端离地面的高度AD是( )
4. 一个不透明的袋中,装有2个黄球、3个红球和5个白球,它们除颜色外都相同.从袋中任意摸出一个球,是白球的概率是( )A、 B、 C、 D、5. 若关于x的一元二次方程4x²-4x+c=0有两个相等实数根,则c的值是( )A、-1 B、1 C、-4 D、46. 不等式组 的解是( )A、x<-1 B、x>-1 C、-1<x<4 D、x>47. 如图,梯子AC的长为2.8米,则梯子顶端离地面的高度AD是( )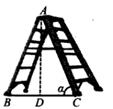 A、 米 B、 米 C、 sinα米 D、 cosα米8. 某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门。已知计划中的建筑材料可建围墙(不包括门)的总长度为50m。设饲养室长为x(m),占地面积为y(m²),则y关于x的函数表达式是( )
A、 米 B、 米 C、 sinα米 D、 cosα米8. 某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门。已知计划中的建筑材料可建围墙(不包括门)的总长度为50m。设饲养室长为x(m),占地面积为y(m²),则y关于x的函数表达式是( ) A、y=-x²+50x B、y= x²+24x C、y= x2+25x D、y= x2+26x9. 已知反比例函数y= (k≠0),当-2≤x≤-1时,y的最大值是3,则当x≥6时,y有( )A、最大值 B、最大值-1 C、最小值 D、最小值-110. 我国古代伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1)。刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法。如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结AG,CF,AG交CF于点P,若AP=2 ,则 的长为( )
A、y=-x²+50x B、y= x²+24x C、y= x2+25x D、y= x2+26x9. 已知反比例函数y= (k≠0),当-2≤x≤-1时,y的最大值是3,则当x≥6时,y有( )A、最大值 B、最大值-1 C、最小值 D、最小值-110. 我国古代伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1)。刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法。如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结AG,CF,AG交CF于点P,若AP=2 ,则 的长为( )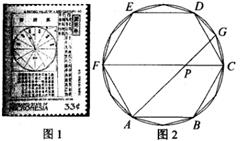 A、 B、 π C、 π D、 π
A、 B、 π C、 π D、 π二、填空题(本题有6小题,每小题5分,共30分)
-
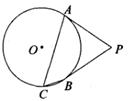
11. 分解因式:m2-2m=。12. 一组数据1,2,x,5,8的平均数是5,则该组数据的中位数是。13. 计算 的结果是。14. 如图,PA,PB是⊙O的切线,A,B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于度。
 15. 如图,在△ABC中,分别以AB,AC为边向外作正方形ABED,ACGF。若点E,A,G在同一直线上,EG=8 ,BC=7,则△ABC的面积为。
15. 如图,在△ABC中,分别以AB,AC为边向外作正方形ABED,ACGF。若点E,A,G在同一直线上,EG=8 ,BC=7,则△ABC的面积为。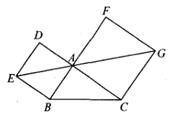 16. 图1是一种指甲剪,该指甲剪利用杠杆原理操作,使用者只需用力按压柄的末端,便可轻易透过锋利的前端刀片剪断指甲,它被按压后示意图如图2所示,上下臂OD=OF,∠CEO=90°,∠ABC=135°,杠杆BC=2 mm,轴承CE=9mm,未使用指甲剪时,点B,C在OD上,且EF比CD长1mm,则OE的长为mm;使用指甲剪时,下压点A,当A'B'∥OF时,两刀片咬合,OD绕点O接逆时针方向旋转到OD'的位置,则OD与CE的交点从开始到结束时移动的距离CG为mm。
16. 图1是一种指甲剪,该指甲剪利用杠杆原理操作,使用者只需用力按压柄的末端,便可轻易透过锋利的前端刀片剪断指甲,它被按压后示意图如图2所示,上下臂OD=OF,∠CEO=90°,∠ABC=135°,杠杆BC=2 mm,轴承CE=9mm,未使用指甲剪时,点B,C在OD上,且EF比CD长1mm,则OE的长为mm;使用指甲剪时,下压点A,当A'B'∥OF时,两刀片咬合,OD绕点O接逆时针方向旋转到OD'的位置,则OD与CE的交点从开始到结束时移动的距离CG为mm。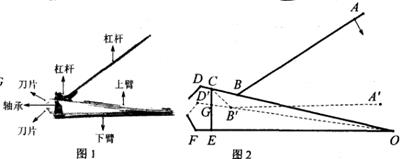
三、解答题(本题有8小题,共80分.)
-
17. 计算:(1)、|-3|- +(π-2020)0-(-1)
(2)、(2a+1)2-4a(a-1)18. 如图,在四边形ABCD中,∠A=90°,对角线BD平分∠ABC,且BD=BC,CE⊥BD于点E。 (1)、求证:△ABD≌△EBC。(2)、当∠ADB=60°时,求∠DCE的度数。19. 某校在开展读书交流活动中,全体师生积极捐书,为了解所捐书籍的种类,对部分书籍进行了抽样调查,张老师根据调查数据绘制了如下不完整的统计图。
(1)、求证:△ABD≌△EBC。(2)、当∠ADB=60°时,求∠DCE的度数。19. 某校在开展读书交流活动中,全体师生积极捐书,为了解所捐书籍的种类,对部分书籍进行了抽样调查,张老师根据调查数据绘制了如下不完整的统计图。
请根据统计图回答下列问题:
(1)、本次抽样调查的书籍有多少本?(2)、试求图1中表示文学类书籍的扇形圆心角的度数,并补全条形统计图。(3)、本次活动师生共捐书1600本,请估计有多少本科普类书籍?20. 如图,在方格纸中,点A,B都在格点上,请按要求画图。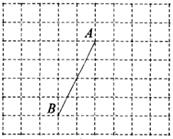 (1)、在图1中画出一个以AB为腰的格点等腰△ABC。(2)、在图2中画出一个以AB为边的格点 ABCD,且其中一个内角为45°。21. 如图,抛物线y=-x²+bx+4交y轴于点B,顶点为M,BA⊥y轴,交抛物线于点A。已知该抛物线的对称轴为直线x= 。
(1)、在图1中画出一个以AB为腰的格点等腰△ABC。(2)、在图2中画出一个以AB为边的格点 ABCD,且其中一个内角为45°。21. 如图,抛物线y=-x²+bx+4交y轴于点B,顶点为M,BA⊥y轴,交抛物线于点A。已知该抛物线的对称轴为直线x= 。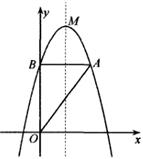 (1)、求b的值和点M的坐标。(2)、将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),则m的取值范围为。22. 如图,在△ABC中,∠ACB=90°,点D在BC边上(不包括端点B,C) ,过A,C,D三点的⊙O交AB于另一点E,连结AD,DE,CE,且CE⊥AD于点G,过点C作CF∥DE交AD于点F,连结EF。
(1)、求b的值和点M的坐标。(2)、将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),则m的取值范围为。22. 如图,在△ABC中,∠ACB=90°,点D在BC边上(不包括端点B,C) ,过A,C,D三点的⊙O交AB于另一点E,连结AD,DE,CE,且CE⊥AD于点G,过点C作CF∥DE交AD于点F,连结EF。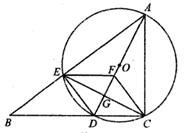 (1)、求证:四边形DCFE是菱形。(2)、当tan∠AEF= ,AC=4时,求⊙O的直径长。23. 下表是小丽在某路口统计20分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊。
(1)、求证:四边形DCFE是菱形。(2)、当tan∠AEF= ,AC=4时,求⊙O的直径长。23. 下表是小丽在某路口统计20分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊。电瓶车
公交车
货车
小轿车
合计(车流总量)
(第一时段)8:50~9:00
m
86
161
(第二时段)9:00~9:10
7n
m
n
99
合计
30
185
(1)、根据表格信息,在表格中填写第一时段电瓶车和货车的数量。(2)、在第二时段内,电瓶车和公交车的车辆数之和恰好是第二时段车流总量的一半,且两个时段的电瓶车总数为170辆。①求m,n的值。
②因为第二时段内车流总量较多,造成了交通拥堵现象,据估计,该时段内,每增加1辆公交车,可减少8辆小轿车和5辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?
24. 如图,在平面直角坐标系中,直线y= x+15分别交x轴、y轴于点A,B,交直线y= x于点M。动点C在直线AB上以每秒3个单位的速度从点A向终点B运动,同时,动点D以每秒a个单位的速度从点0沿OA的方向运动,当点C到达终点B时,点D同时停止运动.设运动时间为t秒。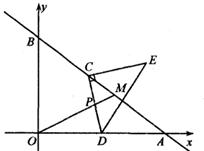 (1)、求点A的坐标和AM的长。(2)、当t=5时,线段CD交OM于点P,且PC=PD,求a的值。(3)、在点C的整个运动过程中,
(1)、求点A的坐标和AM的长。(2)、当t=5时,线段CD交OM于点P,且PC=PD,求a的值。(3)、在点C的整个运动过程中,①直接用含t的代数式表示点C的坐标。
②利用(2)的结论,以C为直角顶点作等腰直角△CDE(点C,D,E按逆时针顺序排列)。当OM与△CDE的一边平行时,求所有满足条件的t的值。