黑龙江省克东县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-05-20 类型:期末考试
一、单选题
-
1. 下面四个图形中∠1与∠2是对顶角的是( )A、
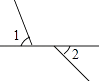 B、
B、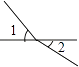 C、
C、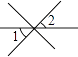 D、
D、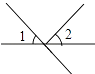 2. 下列事件中,最适合采用全面调查的是( )A、对全国中学生节水意识的调查 B、对某批次灯泡的使用寿命的调查 C、对某个班级全体学生出生日期的调查 D、对春节联欢晚会收视率的调查3. 在平面直角坐标系内,点P(a,a+3)的位置一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 实数a,b在数轴上对应点的位置如图所示,化简|a|+ 的结果是( )
2. 下列事件中,最适合采用全面调查的是( )A、对全国中学生节水意识的调查 B、对某批次灯泡的使用寿命的调查 C、对某个班级全体学生出生日期的调查 D、对春节联欢晚会收视率的调查3. 在平面直角坐标系内,点P(a,a+3)的位置一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 实数a,b在数轴上对应点的位置如图所示,化简|a|+ 的结果是( )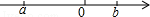 A、﹣2a-b B、2a﹣b C、﹣b D、b5. 由 可以得到用x表示y的式子为( )A、 B、 C、 D、6. 下列说法中正确的个数是( )
A、﹣2a-b B、2a﹣b C、﹣b D、b5. 由 可以得到用x表示y的式子为( )A、 B、 C、 D、6. 下列说法中正确的个数是( )①过一点有且只有一条直线与已知直线垂直;②直线外一点到这条直线的垂线段,叫做点到直线的距离;③能开尽方的数都是有理数:④经过直线外一点有且只有一条直线与这条直线平行;⑤无限小数都是无理数;
A、1 B、2 C、3 D、47. 下列各数中,界于5和6之间的数是( )A、 B、 C、 D、8. 在平面直角坐标系中,第二象限内的点P到x轴的距离是2,到y轴的距离是3,已知线段PQ∥y轴且PQ=5,则点Q的坐标是( )A、 或 B、 或 C、 或 D、 或9. 若关于x的不等式组 无解,则m的取值范围是( )A、 B、 C、 D、10. 甲、乙两人共同解关于x,y的方程组 ,甲正确地解得 乙看错了方程②中的系数c,解得 ,则 的值为( )A、16 B、25 C、36 D、49二、填空题
-
11. 9的算术平方根是 , = , ﹣ = .12. 如图,已知 , , ,则 .
 13. 已知 、 满足方程组 ,则 的值为 .14. 已知 与 的两边分别平行,且 是 的2倍少15°,那么 、∠B的大小分别是、.15. 关于x不等式 仅有三个正整数解,则m的取值范围是.16. 为丰富学生的体育活动,某校计划使用资金2000元购买篮球和足球(两种球都买且钱全部花光).若每个篮球80元,每个足球50元,则该校的购买方案个数为.17. 按一定规律排成的一列数依次为: , , , , , ,…,按此规律下去,这列数中的第2019个数是.
13. 已知 、 满足方程组 ,则 的值为 .14. 已知 与 的两边分别平行,且 是 的2倍少15°,那么 、∠B的大小分别是、.15. 关于x不等式 仅有三个正整数解,则m的取值范围是.16. 为丰富学生的体育活动,某校计划使用资金2000元购买篮球和足球(两种球都买且钱全部花光).若每个篮球80元,每个足球50元,则该校的购买方案个数为.17. 按一定规律排成的一列数依次为: , , , , , ,…,按此规律下去,这列数中的第2019个数是.三、综合题
-
18.(1)、计算: ;(2)、解不等式: ,并在数轴上表示它的解集.19. 完成下面的证明:如图, ,BE和CF分别平分 和 ,求证: .

证明:∵ (已知)
∴ ()
∵BE,CF分别平分 和 (已知)
∴ , ()
∴ ()
∴ ()
20. 解方程组:21. 如图是单位长度为1的正方形网格,若A,B两点的坐标分别为 , .
请解决下列问题:
(1)、在网格图中画出平面直角坐标系,并直接写出点C的坐标.(2)、将图中三角形ABC沿x轴向右平移1个单位,再沿y轴向上平移2个单位后得到三角形 ,则 的坐标为; 的坐标为; 的坐标为;(3)、在y轴上是否存在点P,使得三角形 的面积为4,若存在,请直接写出P点坐标:若不存在,请说明理由.22. 某学校要开展校园艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下两幅不完整的统计图.
请根据图中信息,回答下列问题:
(1)、本次共调查了名学生.(2)、在扇形统计图中,“歌曲”所在扇形的圆心角等于度.(3)、补全条形统计图(并标注频数).(4)、根据以上统计分析,估计该校2000名学生中最喜爱小品的人数约有多少名?23. 如图,已知AE∥BF,∠A=60°,点P为射线AE上任意一点(不与点A重合),BC,BD分别平分∠ABP和∠PBF,交射线AE于点C,点D. (1)、图中∠CBD=°;(2)、当∠ACB=∠ABD时,∠ABC=°;(3)、随点P位置的变化,图中∠APB与∠ADB之间的数量关系始终为 , 请说明理由.24. “一带一路”国际合作高峰论坛期间,我国同30多个国家签署经贸合作协议.某工厂准备生产甲、乙两种商品共6万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.(1)、甲种商品与乙种商品的销售单价各多少元?(2)、若甲、乙两种商品的销售总收入不低于4200万元,则至少销管甲种商品多少万件?
(1)、图中∠CBD=°;(2)、当∠ACB=∠ABD时,∠ABC=°;(3)、随点P位置的变化,图中∠APB与∠ADB之间的数量关系始终为 , 请说明理由.24. “一带一路”国际合作高峰论坛期间,我国同30多个国家签署经贸合作协议.某工厂准备生产甲、乙两种商品共6万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.(1)、甲种商品与乙种商品的销售单价各多少元?(2)、若甲、乙两种商品的销售总收入不低于4200万元,则至少销管甲种商品多少万件?