陕西省2020年初中学业水平考试数学模拟试卷（一）

试卷更新日期：2020-05-20 类型：中考模拟

进入出卷网下载

一、选择题(共10小题，每小题3分，计30分。)

1. $- \frac{27}{64}$ 的立方根是（）

A、 $- \frac{3}{4}$ B、 $\frac{3}{8}$ C、 $- \frac{4}{9}$ D、 $\frac{9}{16}$

查看试题解析
2. 如图，下面关于正六棱柱的视图(主视图、左视图、俯视图)中，画法错误的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，AB∥CD，DA⊥AC，垂足为A，若∠ADC=35°，则∠1的度数为（）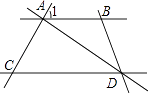

A、65° B、55° C、45° D、35°

查看试题解析
4. 若正比例函数y=(2k-1)x的图象上有一点A(x₁ ， y₁)，且x₁y₁<0，则k的取值范围是（）

A、k< $\frac{1}{2}$ B、k> $\frac{1}{2}$ C、k< $\frac{1}{2}$ 或> $\frac{1}{2}$ D、无法确定

查看试题解析
5. 下列计算正确的是（）

A、(a-b)(-a-b)=a²-b² B、2a³+3a³=5a⁶ C、6x³y²÷3x=2x²y² D、(-2x²)³=-6x³y⁶

查看试题解析
6. 如图，在△ABC中，∠ACB=90°，D为AB边的中点，连接CD并延长至点E，使DE=CD。连接AE，过点B作BF∥DE交AE的延长线于点F。若BF=7，则AB的长为（）

A、3.5 B、7 C、10 D、14

查看试题解析
7. 如果函数y=kx-6和y=-2x+a的图象的交点在第三象限，那么k，a的取值范围是（）

A、k>0，a>-6 B、k>0，a<-6 C、k>0，a>6 D、k<0，a>6

查看试题解析
8. 如图，在矩形ABCD中，点E在AB上，点F在CD上，且BE=2AE，DF=2CF，G，H是对角线AC的三等分点。若四边形EGFH的面积为2，则矩形ABCD的面积为（）

A、36 B、24 C、18 D、12

查看试题解析
9. 如图，点A，B，C，D在⊙O上， $\overset{⌢}{C B}$ = $\overset{⌢}{C D}$ ，∠CAD=35°，∠ACD=55°，则∠AOB=（ )

A、120° B、110° C、90° D、85°

查看试题解析
10. 在平面直角坐标系xOy中，已知点M，N的坐标分别为(-1，2)，(2，1)，若抛物线y=ax²-x+2(a≠0)与线段MN有两个不同的交点，则a的取值范围是（）

A、a≤-1或a≥ $\frac{1}{4}$ B、 $\frac{1}{4}$ ≤a< $\frac{1}{3}$ C、a≤ $\frac{1}{4}$ 或a> $\frac{1}{3}$ D、a≤-1或 $\frac{1}{4}$ ≤a< $\frac{1}{3}$

查看试题解析

二、填空题(共4小题，每小题3分，计12分)

11. 如图，数轴上点A，B分别表示数a，b，则a+bb-a。(填“>”“<”或“=”)

查看试题解析
12. 如图，正八边形和正五边形按如图方式拼接在一起，则∠ABC的度数为。

查看试题解析
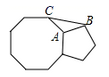13. 如图，已知反比例函数y= $\frac{k}{x}$ (k<0) 的图象经过Rt△OAB斜边OA的中点D(-6，a)，且与直角边AB相交于点C。若△AOC的面积为18，则k的值为。

查看试题解析
14. 如图，在△ABC中，AB=AC=8，BC=4 $\sqrt{3}$ ，D为BC边的中点，E，F分别是线段AC，AD上的动点，且AF=CE，则BE+CF的最小值是。

查看试题解析

三、解答题(共11小题，计78分。)

15. 计算：(π-5)⁰+ $\sqrt{2}$ × $\sqrt{6}$ +( $\frac{1}{2}$ )^-1

查看试题解析
16. 解分式方程： $\frac{x}{2 - x}$ =4- $\frac{7}{x - 2}$

查看试题解析
17. 如图，在△ABC中，D为AB边上一点，求作⊙O，使得⊙O经过D，C两点，且与直线AB相切于点D。(不写作法，保留作图痕迹)

查看试题解析
18. 如图，在平行四边形ABCD中，E为BC边上一点，且∠B=∠AEB。求证：AC=ED。

查看试题解析
19. 某县教育系统为更好地落实对《习近平关于新时代中国特色社会主义思想》的理论学习，
抽取了某校部分教师进行了笔试理论测试，并根据测试成绩绘制成下面两幅不完整的统计图：

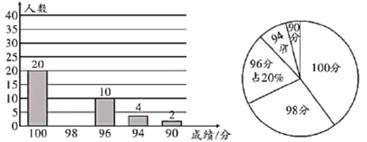
请根据统计图中提供的信息，回答下面的问题：

(1)、本次测试成绩为98分的教师有人，并补全条形统计图；

(2)、本次测试成绩的中位数是，众数是；

(3)、若该县共有教师5600名，根据本次成绩估计该县有多少名教师全部掌握《习近平关于新时代中国特色社会主义思想》的理论知识。

查看试题解析
20. 西安市某中学在创建“特色校园”的活动中，将本校的办学理念做成宣传牌(AB)，放置在教学楼的顶部(如图所示)．小明在操场上的点D处，用1米高的测角仪CD，从点C测得宣传牌的底部B的仰角为30°，然后向教学楼正方向走了5米到达点F处，又从点E测得宣传牌的顶部A的仰角为45°。已知教学楼高BM=16米，且点A，B，M在同一直线上，求宣传牌AB的高度。(结果保留根号)

查看试题解析
21. “绿水青山就是金山银山”．为了保护环境提高樱桃树产量，某果农计划从甲、乙两个仓库用汽车向A，B两个果园运送有机化肥．甲、乙两个仓库分别可运出70吨和90吨有机化肥；A，B两个果园分别需用100吨和60吨有机化肥．两个仓库到A，B两个果园的路程如下表所示：

果园

路程/千米

甲仓库

乙仓库

A

15

25

B

20

20

设甲仓库运往A果园x吨有机化肥，若汽车每吨每千米的运费为2元。

(1)、设总运费为y元，求y关于x的函数表达式。

(2)、当甲仓库运往A果园多少吨有机化肥时，总运费最省？最省的总运费是多少元？

查看试题解析
22. 某超市在“双十二”期间开展优惠活动，凡购物者可以通过转动转盘的方式享受折扣优惠，本次活动共有两种方式，方式一：转动转盘甲，指针指向B区域时，所购买物品享受8折优惠，指针指向其他区域无优惠；方式二：同时转动转盘甲和转盘乙，若两个转盘的指针指向每个区域的字母相同，所购买物品享受6折优惠，其他情况无优惠。在每个转盘中，指针指向每个区域的可能性相同(若指针指向分界线，则重新转动转盘)

(1)、若顾客选择方式一，则享受8折优惠的概率为；

(2)、若顾客选择方式二，请用画树状图法或列表法列出所有可能，并求顾客享受6折优惠的概率。

查看试题解析
23. 如图，在△ABC中，∠B=60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点M ， CM交⊙O于点D ．

(1)、求证：AM=AC；

(2)、若AC=3，求MC的长．

查看试题解析
24. 如图，已知二次函数y=ax²+2x+c的图象经过点C(0，3)，与x轴分别交于点A，点B(3，0)，P是直线BC上方的抛物线上一动点。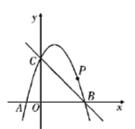

(1)、求二次函数y=ax²+2x+c的解析式。

(2)、连接PO，PC，并把△POC沿y轴翻折，得到四边形POP'C．若四边形POP'C为菱形，请求出此时点P的坐标。

(3)、当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积。

查看试题解析
25. 问题探究

(1)、如图1，点A，B在直线l的同侧，请你在直线l上找一点P，使得AP+BP的值最小(不需要说明理由)；

(2)、尝试体验：如图2，菱形ABCD的边长为6，对角线AC=6 $\sqrt{3}$ ，点E，F在AC上，且EF=2，求DE+BF的最小值。

(3)、解决应用如图3，在四边形ABCD中，AB=AD=6，∠BAD=60°，∠BCD=120°，四边形ABCD的周长是否存在最大值？若存在，请求出最大值；若不存在，请说明理由。

查看试题解析

果园	路程/千米
果园	甲仓库	乙仓库
A	15	25
B	20	20