黑龙江省哈尔滨市南岗区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-05-20 类型:期末考试
一、单选题
-
1. 数据2,3,5,5,4的众数是( )A、2 B、3 C、4 D、52. 一元一次不等式组 的解集在数轴上表示为( ).A、
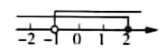 B、
B、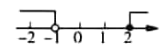 C、
C、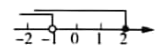 D、
D、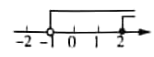 3. 某企业车间有50名工人,某一天他们生产的机器零件个数统计如下表:
3. 某企业车间有50名工人,某一天他们生产的机器零件个数统计如下表:零件个数(个)
5
6
7
8
人数(人)
3
15
22
10
表中表示零件个数的数据中,中位数是( ).
A、5个 B、6个 C、7个 D、8个4. 若正多边形的一个内角是150°,则该正多边形的边数是( )A、6 B、12 C、16 D、185. 某市连续7天的最高气温为: , , , , , , .这组数据的平均数是( ).A、 B、 C、 D、6. 若 ,则下列式子不正确的是( ).A、 B、 C、 D、7. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD8. 若 ,则 的值( ).A、 B、2 C、-4 D、49. 下列四个命题是假命题的是( ).A、斜边和一条直角边分别相等的两个直角三角形全等 B、有两边和一角对应相等的两上三角形全等 C、角的平分线上的点到角的两边的距离相等 D、全等三角形的对应角相等10. 对于不等式组 ,下列说法正确的是( )A、此不等式组的正整数解为1,2,3 B、此不等式组的解集为 C、此不等式组有5个整数解 D、此不等式组无解二、填空题
-
11. 把方程 改写成用含 的式子表示 的形式为 .12. 人数相同的七年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差分别为 , ,则学生成绩较为稳定的班级是班.13. 已知 是方程 的解,则 的值为.14. 某班体育委员对本班40名学生一周锻炼时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周锻炼时间的中位数是小时.
 15. 两人练习跑步,如果乙先跑16米,甲8秒可追上乙,如果乙先跑2秒钟,则甲4秒可追上乙,求甲乙二人每秒各跑多少米.设甲每秒跑 米,乙每秒跑 米,依题意,可列方程组为.16. 如图, ,且 .点 是 上的两点, .若 ,则 的长为.
15. 两人练习跑步,如果乙先跑16米,甲8秒可追上乙,如果乙先跑2秒钟,则甲4秒可追上乙,求甲乙二人每秒各跑多少米.设甲每秒跑 米,乙每秒跑 米,依题意,可列方程组为.16. 如图, ,且 .点 是 上的两点, .若 ,则 的长为. 17. 超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如下表:
17. 超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如下表:测试项目
创新能力
综合知识
语言表达
测试成绩(分数)
70
80
95
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是分.
18. 已知: 分别是 的高,角平分线, ,则 的度数为度.19. 甲乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超过50元的部分按95%收费,则顾客累计购物金额要超过元时,在甲商场购物花费比在乙商场购物花费少.20. 如图, 为 的中线,点 在 的延长线上的点,连接 ,且 ,过点 作 于点 ,连接 ,若 ,则 的长为.
三、综合题
-
21. 解下列方程组:(1)、(2)、22. 解下列不等式:(1)、(2)、23. 为提高节水意识,小明随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
每天用水折线统计图第3天用水情况条形统计图
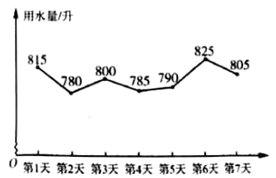
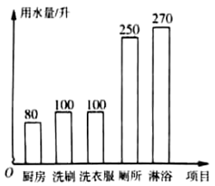 (1)、填空:这7天内小明家里每天用水量的平均数为升、中位数为升;(2)、求第3天小明家淋浴的水占这一天总用水量的百分比.24. 已知:在 中, ,点 在 的内部,连接 ,且 , .(1)、如图1,求 的度数;
(1)、填空:这7天内小明家里每天用水量的平均数为升、中位数为升;(2)、求第3天小明家淋浴的水占这一天总用水量的百分比.24. 已知:在 中, ,点 在 的内部,连接 ,且 , .(1)、如图1,求 的度数; (2)、如图2,延长 交 于点 ,延长 交 于点 ,若 ,求 的度数.
(2)、如图2,延长 交 于点 ,延长 交 于点 ,若 ,求 的度数. 25. 某市正在创建“全国文明城市”,光明学校拟举办“创文知识”抢答案,欲购买 两种奖品以抢答者.如果购买 种25件, 种20件,共需480元;如果购买 种15件, 种25件,共需340元.(1)、 两种奖品每件各多少元?(2)、现要购买 两种奖品共100件,总费用不超过1120元,那么最多能购买 种奖品多少件?26. “综合与实践”学习活动准备制作一组三角形,记这些三角形分别为 ,用记号 表示一个满足条件的三角形,如(2,4,4)表示边长分别为2,4,4个单位长度的一个三角形.(1)、若这些三角形三边的长度为大于0且小于3的整数个单位长度,请用记号写出所有满足条件的三角形;(2)、如图, 是 的中线,线段 的长度分别为2个,6个单位长度,且线段 的长度为整数个单位长度,过点 作 交 的延长线于点 .
25. 某市正在创建“全国文明城市”,光明学校拟举办“创文知识”抢答案,欲购买 两种奖品以抢答者.如果购买 种25件, 种20件,共需480元;如果购买 种15件, 种25件,共需340元.(1)、 两种奖品每件各多少元?(2)、现要购买 两种奖品共100件,总费用不超过1120元,那么最多能购买 种奖品多少件?26. “综合与实践”学习活动准备制作一组三角形,记这些三角形分别为 ,用记号 表示一个满足条件的三角形,如(2,4,4)表示边长分别为2,4,4个单位长度的一个三角形.(1)、若这些三角形三边的长度为大于0且小于3的整数个单位长度,请用记号写出所有满足条件的三角形;(2)、如图, 是 的中线,线段 的长度分别为2个,6个单位长度,且线段 的长度为整数个单位长度,过点 作 交 的延长线于点 .
①求 的长度;
②请直接用记号表示 .
27. 已知:在 中, ,点 在 上,连接 , .(1)、如图1,求证: ; (2)、如图2,点 为 的中点,过点 作 的垂线分别交 的延长线, 的延长线, 于点 ,求证: ;
(2)、如图2,点 为 的中点,过点 作 的垂线分别交 的延长线, 的延长线, 于点 ,求证: ; (3)、如图3,在(2)的条件下,过点 分别作 于点 于点 ,若 , ,求 的面积.
(3)、如图3,在(2)的条件下,过点 分别作 于点 于点 ,若 , ,求 的面积.