上海市松江区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-20 类型:期末考试
一、单选题
-
1. 直线 的截距是 ( )A、—3 B、—2 C、2 D、32. 如果关于 的方程 有解,那么实数 的取值范围是( )A、 B、 C、 D、3. 下列说法正确的是( )A、 是二项方程 B、 是二元二次方程 C、 是分式方程 D、 是无理方程4. 下列事件中,属于确定事件的是( )A、抛掷一枚质地均匀的骰子,正面向上的点数是6 B、抛掷一枚质地均匀的骰子,正面向上的点数大于6 C、抛掷一枚质地均匀的骰子,正面向上的点数小于6 D、抛掷一枚质地均匀的骰子6次,“正面向上的点数是6”至少出现一次5. 如果平行四边形 两条对角线的长度分别为 ,那么 边的长度可能是( )A、 B、 C、 D、6. 已知平行四边形 中, ,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )A、 B、 C、 D、
二、填空题
-
7. 已知一次函数 ,那么8. 已知函数 ,当 时,函数值 的取值范围是9. 将直线 向上平移1个单位,那么平移后所得直线的表达式是10. 二项方程 在实数范围内的解是11. 用换元法解方程 时,如果设 ,那么所得到的关于 的整式方程为12. 如果 是关于 的方程 的增根,那么实数 的值为13. 不透明的布袋里有2个黄球、3个红球、5个白球,它们除颜色外其它都相同,那么从布袋中任意摸出一球恰好为红球的概率是 .14. 一个多边形每个外角都是 ,则这个多边形是边形.15. 如果向量 ,那么四边形 的形状可以是(写出一种情况即可)16. 写出一个轴对称图形但不是中心对称图形的四边形:17. 已知正方形 的边长为1,如果将向量 的运算结果记为向量 ,那么向量 的长度为18. 已知四边形 是矩形,点 是边 的中点,以直线 为对称轴将 翻折至 ,联结 ,那么图中与相等的角的个数为

三、综合题
-
19. 解方程:20. 解方程21. 已知向量 ,(如图),请用向量的加法的平行四边形法则作向量 (不写作法,画出图形)
 22. 甲、乙两位同学同时从学校出发,骑自行车前往距离学校20千米的郊野公园。已知甲同学比乙同学平均每小时多骑行2千米,甲同学在路上因事耽搁了30分钟,结果两人同时到达公园。问:甲、乙两位同学平均每小时各骑行多少千米?23. 已知 (如图),点 分别在边 上,且四边形 是菱形
22. 甲、乙两位同学同时从学校出发,骑自行车前往距离学校20千米的郊野公园。已知甲同学比乙同学平均每小时多骑行2千米,甲同学在路上因事耽搁了30分钟,结果两人同时到达公园。问:甲、乙两位同学平均每小时各骑行多少千米?23. 已知 (如图),点 分别在边 上,且四边形 是菱形 (1)、请使用直尺与圆规,分别确定点 的具体位置(不写作法,保留画图痕迹);(2)、如果 ,点 在边 上,且满足 ,求四边形 的面积;(3)、当 时,求 的值。24. 为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图1表达的是小贾的爸爸行驶的路程y(米)与行驶时间x(分钟)的变化关系
(1)、请使用直尺与圆规,分别确定点 的具体位置(不写作法,保留画图痕迹);(2)、如果 ,点 在边 上,且满足 ,求四边形 的面积;(3)、当 时,求 的值。24. 为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图1表达的是小贾的爸爸行驶的路程y(米)与行驶时间x(分钟)的变化关系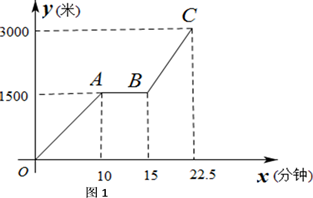
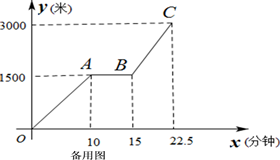 (1)、求线段BC所表达的函数关系式;(2)、如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分钟行驶,当小贾与爸爸相距100米是,求小贾的行驶时间;(3)、如果小贾的行驶速度是 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出 的取值范围。25. 在梯形 中, ,点 在直线 上,联结 ,过点 作 的垂线,交直线 与点 ,
(1)、求线段BC所表达的函数关系式;(2)、如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分钟行驶,当小贾与爸爸相距100米是,求小贾的行驶时间;(3)、如果小贾的行驶速度是 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出 的取值范围。25. 在梯形 中, ,点 在直线 上,联结 ,过点 作 的垂线,交直线 与点 ,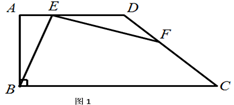
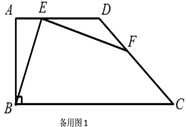
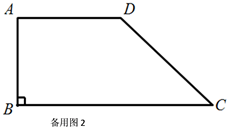 (1)、如图1,已知 ,求证: ;(2)、已知: ,
(1)、如图1,已知 ,求证: ;(2)、已知: ,① 当点 在线段 上,求证: ;
② 当点 在射线 上,①中的结论是否成立?如果成立,请写出证明过程;如果不成立,简述理由.