上海市普陀区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-05-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数中，一次函数是（）．

A、 $y = x$ B、 $y = k x + b$ C、 $y = \frac{1}{x} + 1$ D、 $y = x^{2} - 2 x$

查看试题解析
2. 下列方程中，有实数根的方程是（　　）

A、x⁴+16＝0 B、x²+2x+3＝0 C、 $\frac{x^{2} - 4}{x - 2} = 0$ D、 $\sqrt{x} + \sqrt{x - 1} = 0$

查看试题解析
3. 在同一平面直角坐标系中的图像如图所示，则关于 $k_{2} x < k_{1} x + b$ 的不等式的解为（）．

A、 $x > - 1$ B、 $x < - 2$ C、 $x < - 1$ D、无法确定

查看试题解析
4. 下列事件中，属于随机事件的是（）．

A、凸多边形的内角和为 $500 °$ B、凸多边形的外角和为 $360 °$ C、四边形绕它的对角线交点旋转 $180 °$ 能与它本身重合 D、任何一个三角形的中位线都平行于这个三角形的第三边

查看试题解析
5. 化简 $(\vec{A B} - \vec{C D}) + (\vec{B E} - \vec{D E})$ 的结果是（）．

A、 $\vec{C A}$ B、 $\vec{A C}$ C、 $\vec{0}$ D、 $\vec{A E}$

查看试题解析
6. 如图，在四边形ABCD中，AC与BD相交于点O，AD∥BC，AC＝BD，那么下列条件中不能判定四边形ABCD是矩形的是（　　）

A、AD＝BC B、AB＝CD C、∠DAB＝∠ABC D、∠DAB＝∠DCB

查看试题解析

二、填空题

7. 若一次函数 $y = (2 - k) x + 1$ 中， $y$ 随 $x$ 的增大而减小，则 $k$ 的取值范围是．

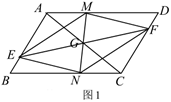
查看试题解析
8. 已知直线 $y = (k - 2) x + 3$ 与直线 $y = 3 x - 2$ 平行，那么 $k =$ ．

查看试题解析
9. 方程 $x^{3} + 2 = 0$ 在实数范围内的解是．

查看试题解析
10. 方程 $\frac{x^{2}}{x - 2} = \frac{4}{x - 2}$ 的解是．

查看试题解析
11. 用换元法解方程 $\frac{x^{2} - 1}{x} + \frac{2 x}{x^{2} - 1} = 3$ 时，如果设 $\frac{x^{2} - 1}{x} = y$ ，那么得到关于 $y$ 的整式方程为．

查看试题解析
12. 将二元二次方程 $x^{2} - 5 x y + 6 y^{2} = 0$ 化为两个一次方程为．

查看试题解析
13. 已知菱形两条对角线的长分别为12和16，则这个菱形的周长为.

查看试题解析
14. 如图，在四边形 $A B C D$ 中， $A B \neq C D$ ， $E$ ， $F$ ， $G$ ， $H$ 分别是 $A B$ ， $B D$ ， $C D$ ， $A C$ 的中点，要使四边形 $E F G H$ 是菱形，四边形 $A B C D$ 还应满足的一个条件是．

查看试题解析
15. 在5张完全相同的卡片上分别画上等边三角形、平行四边形、直角梯形、正方形和圆．在看不见图形的情况下随机摸出1张，这张卡片上的图形是中心对称图形的概率是．

查看试题解析
16. 已知在等腰梯形 $A B C D$ 中， $C D / / A B$ ， $A D = B C$ ，对角线 $A C ⊥ B D$ ，垂足为 $O$ ，若 $C D = 3$ ， $A B = 8$ ，梯形的高为．

查看试题解析
17. 如图，正方形ABCD的边长为6，点E，F分别在AB，AD上，若CE= $3 \sqrt{5}$ ，且∠ECF=45°，则CF的长为．

查看试题解析
18. 如图，在平行四边形ABCD中，AC与BD相交于点O，∠AOB=60°，BD=4，将△ABC沿直线AC翻折后，点B落在点E处，那么S_△_AED=

查看试题解析

三、综合题

19. 解方程： $\sqrt{2 x - 5} = 1 - \sqrt{x + 1}$

查看试题解析
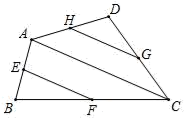
20. 解方程组： ${\begin{array}{l} x^{2} - 4 y^{2} = 12 ① \\ x + 2 y = 6 ② \end{array}$ ．

查看试题解析
21. 如图，点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点．

(1)、如果图中线段都可画成有向线段，那么在这些有向线段所表示的向量中，与向量 $\vec{E F}$ 相等的向量是；

(2)、设 $\vec{A B}$ ＝ $\vec{a}$ ， $\vec{B C}$ ＝ $\vec{b}$ ， $\vec{A D}$ ＝ $\vec{c}$ ．试用向量 $\vec{a}$ ， $\vec{b}$ 或 $\vec{c}$ 表示下列向量： $\vec{A C}$ ＝； $\vec{D C}$ ＝．

(3)、求作： $\vec{B C}$ $- \vec{D G}$ ．（请在原图上作图，不要求写作法，但要写出结论）

查看试题解析
22. 某校学生在“蓝天下的至爱”帮困活动中，纷纷拿零花钱，参加募捐活动．甲班学生共募捐840元，乙班学生共募捐1000元，乙班学生的数比甲班学生的人均捐款数多5元，且人数比甲班少2名，求甲班和乙班学生的人数．

查看试题解析
23. 某边防局接到情报，近海处有一可疑船只 $A$ 正向公海方向行驶，边防局迅速派出快艇 $B$ 追赶（如图1）．图2中 $l_{1}$ 、 $l_{2}$ 分别表示两船相对于海岸的距离 $s$ （海里）与追赶时间 $t$ （分）之间的关系．

$l_{2}$

(1)、求 $l_{1}$ 、的函数解析式；

(2)、当 $A$ 逃到离海岸12海里的公海时， $B$ 将无法对其进行检查．照此速度， $B$ 能否在 $A$ 逃入公海前将其拦截？若能，请求出此时 $B$ 离海岸的距离；若不能，请说明理由．

查看试题解析
24. 已知：如图1，在 $▱ A B C D$ 中，点 $G$ 为对角线 $A C$ 的中点，过点 $G$ 的直线 $E F$ 分别交边 $A B$ 、 $C D$ 于点 $E$ 、 $F$ ，过点 $G$ 的直线 $M N$ 分别交边 $A D$ 、 $B C$ 于点 $M$ 、 $N$ ，且 $∠ A G E = ∠ C G N$ ．

(1)、求证：四边形 $E N F M$ 为平行四边形；

(2)、如图2，当四边形 $E N F M$ 为矩形时，求证： $B E = B N$ ．

查看试题解析
25. 如图，已知直角梯形 $A B C D$ ， $A D / / B C$ ， $∠ D C B = 90 °$ ，过点 $A$ 作 $A H ⊥ B C$ ，垂足为点 $H$ ， $C D = 4$ ， $B H = 2$ ，点 $F$ 是 $C D$ 边上的一动点，过 $F$ 作线段 $A B$ 的垂直平分线，交 $A B$ 于点 $E$ ，并交射线 $B C$ 于点 $G$ ．

(1)、如图1，当点 $F$ 与点 $C$ 重合时，求 $B C$ 的长；

(2)、设 $A D = x$ ， $D F = y$ ，求 $y$ 与 $x$ 的函数关系式，并写出定义域；

(3)、如图2，联结 $D E$ ，当 $△ D E F$ 是等腰三角形时，求 $A D$ 的长．

查看试题解析