上海市静安区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-20 类型:期末考试
一、单选题
-
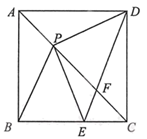
1. 下列方程中,是分式方程的为( )A、 B、 C、 D、2. 下列函数中,图像不经过第二象限的是( )A、 B、 C、 D、3. 如果点 在正比例函数 的图像上,那么下列等式一定成立的是( )A、 B、 C、 D、4. 下列关于 的方程中,有实数解的为( )A、 B、 C、 D、5. 从 、 、 、 这四个代数式中任意抽取一个,下列事件中为确定事件的是( )A、抽到的是单项式 B、抽到的是整式 C、抽到的是分式 D、抽到的是二次根式6. 如图,在四边形 中, 与 相交于点 , ,那么下列条件中不能判定四边形 是菱形的为( )
 A、∠OAB=∠OBA B、∠OBA=∠OBC C、AD∥BC D、AD=BC
A、∠OAB=∠OBA B、∠OBA=∠OBC C、AD∥BC D、AD=BC二、填空题
-
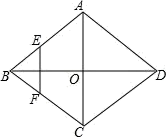
7. 直线 的截距是 .8. 函数 的定义域是 .9. 方程 的根是 .10. 方程 的根是 .11. 已知方程 ,如果设 ,那么原方程可以变形成关于 的方程为 .12. 如果多边形的每个外角都是 ,那么这个多边形的边数是 .13. 与向量 相等的向量是 .14. 在矩形 中, 与 相交于点 , ,那么 的度数为, .15. 如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF= ,BD=4,则菱形ABCD的边长为.
 16. 一个不透明的布袋中装有分别标着数字1,2,3,4的四张卡片,现从袋中随机摸出两张卡片,则这两张卡片上的数字之和大于5的概率为.17. 已知某汽车油箱中的剩余油量 y (升)是该汽车行驶时间 t (小时)的一次函数,其关系如下表:
16. 一个不透明的布袋中装有分别标着数字1,2,3,4的四张卡片,现从袋中随机摸出两张卡片,则这两张卡片上的数字之和大于5的概率为.17. 已知某汽车油箱中的剩余油量 y (升)是该汽车行驶时间 t (小时)的一次函数,其关系如下表:t (小时)
…
y (升)
…
由此可知,汽车行驶了小时, 油箱中的剩余油量为 升.
18. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B= .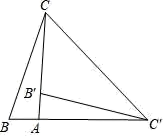
三、综合题
-
19. 计算: .20. 解方程: .21. 解方程组:22. 如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设 .
 (1)、用向量 表示下列向量: ;(2)、求作: (保留作图痕迹,写出结果,不要求写作法)23. 如图,在四边形 中, ,点 为 的中点.
(1)、用向量 表示下列向量: ;(2)、求作: (保留作图痕迹,写出结果,不要求写作法)23. 如图,在四边形 中, ,点 为 的中点.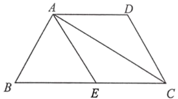 (1)、求证:四边形 是菱形;(2)、联结 ,如果 平分 , 求 的长.24. 某工厂生产的 1640 件新产品,需要精加工后才能投放市场.现把精加工新产品的任务分给甲、乙两人,甲加工新产品的数量要比乙多 5% .
(1)、求证:四边形 是菱形;(2)、联结 ,如果 平分 , 求 的长.24. 某工厂生产的 1640 件新产品,需要精加工后才能投放市场.现把精加工新产品的任务分给甲、乙两人,甲加工新产品的数量要比乙多 5% .
(1)、求甲、乙两人各需加工多少件新产品;(2)、已知乙比甲平均每天少加工 20 件新产品,用时比甲多用 1 天时间.求甲平均每天加工多少件新产品.