浙江省杭州市萧山区2020年数学中考一模试卷
试卷更新日期：2020-05-20 类型：中考模拟
一、单选题
-
1. 下列四个数，表示无理数的是（ ）A、sin30° B、π C、 D、2. 下列四种标志图案中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
3. 下列各式正确的是（ ）A、6a2﹣5a2＝a2 B、（2a）2＝2a2 C、﹣2（a﹣1）＝﹣2a+1 D、（a+b）2＝a2+b24. 如图所示，直线a、b、c、d的位置如图所示，若∠1＝125°，∠2＝125°，∠3＝135°，则∠4的度数为（ ）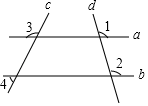
A、45° B、55° C、60° D、65°5. 某工艺品厂草编车间共有16名工人，为了了解每个工人的日均生产能力，随机调查了某天每个工人的生产件数，获得数据如下表：生产件数（件）
10
11
12
13
14
15
人数（人）
1
5
4
3
2
1
则这一天16名工人生产件数的众数和中位数分别是（ ）
A、5件、11件 B、12件、11件 C、11件、12件 D、15件、14件6. 如图，▱ABCD的周长为22m，对角线AC、BD交于点O，过点O与AC垂直的直线交边AD于点E，则△CDE的周长为（ ）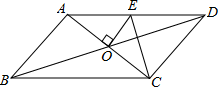
A、8cm B、9cm C、10cm D、11cm7. 一个圆锥的主视图是边长为6cm的正三角形，则这个圆锥的侧面积等于（ ）A、36 πcm2 B、24πcm2 C、18πcm2 D、12 πcm28. 如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，DF⊥AB交AC于点G，反比例函数y＝ （x＞0）经过线段DC的中点E，若BD＝4，则AG的长为（ ）
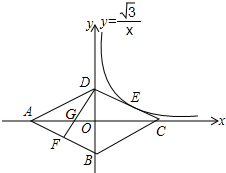A、 B、 +2 C、2 +1 D、 +1二、填空题
-
9. 使 有意义的x的取值范围是 ．
10. 若x＝﹣1是关于x的方程2x+3m﹣7＝0的解，则m的值为.11. 青盐铁路（青岛一盐城），是我国“八纵八横”高速铁路网中第一纵“沿海通道”的一部分，全长428.752千米.数据428.752千米用科学记数法表示为米.12. 在一个不透明的盒子中装有红、白两种除颜色外完全相同的球，其中有a个白球和3个红球，若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子．通过大量重复试验后，发现摸到红球的频率稳定在20%左右，则a的值约为 ．13. 长、宽分别为a、b的矩形，它的周长为14，面积为10，则a2b+ab2的值为.14. 如图，CE、BF分别是△ABC的高线，连接EF，EF＝6，BC＝10，D、G分别是EF、BC的中点，则DG的长为.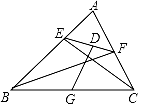
15. 如图，在Rt△ABC中，∠ABC＝90°，AB＝3，BC＝1.将边BA绕点B顺时针旋转90°得线段BD，再将边CA绕点C顺时针旋转90°得线段CE，连接DE，则图中阴影部分的面积是.
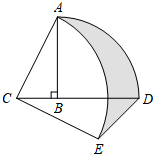16. 如图，已知△ABC中，∠BAC＝120°，AB＝AC＝2 .D为BC边一点，且BD：DC＝1：2.以D为一个点作等边△DEF，且DE＝DC连接AE，将等边△DEF绕点D旋转一周，在整个旋转过程中，当AE取得最大值时AF的长为.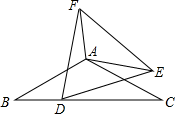
三、解答题
-
17. 解不等式 ，并把它的解集在数轴上表示出来：
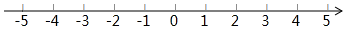18. 先化简，再求值：（x﹣3）2+2（x﹣2）（x+7）﹣（x+2）（x﹣2），其中x2+2x﹣3＝0.19. 已知关于x方程x2﹣6x+m+4＝0有两个实数根x1 ， x2(1)、求m的取值范围；(2)、若x1＝2x2 ， 求m的值.20.某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图．
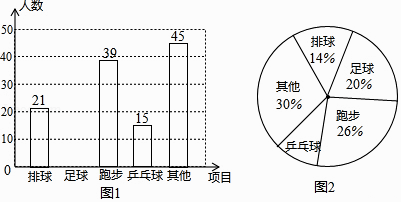
请结合以上信息解答下列问题：
(1)、m=；(2)、请补全上面的条形统计图；(3)、在图2中，“乒乓球”所对应扇形的圆心角的度数为；(4)、已知该校共有1200名学生，请你估计该校约有名学生最喜爱足球活动．21. “2019大洋湾盐城马拉松”的赛事共有三项：A，“全程马拉松”、B，“半程马拉松”、C．“迷你健身跑”，小明和小刚参与了该项赛事的志愿者服务工作，组委会随机将志愿者分配到三个项目组．(1)、小明被分配到“迷你健身跑”项目组的概率为；(2)、求小明和小刚被分配到不同项目组的概率．22. 如图，在四边形ABCD中，AD∥BC，∠ABC＝∠ADC，对角线AC、BD交于点O，AO＝BO，DE平分∠ADC交BC于点E，连接OE.
(1)、求证：四边形ABCD是矩形；(2)、若AB＝2，求△OEC的面积.23. 某公司研发生产的560件新产品需要精加工后才能投放市场.现由甲、乙两个工厂来加工生产，已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍，并且加工生产240件新产品甲工厂比乙工厂少用4天.(1)、求甲、乙两个工厂每天分别可加工生产多少件新产品？(2)、若甲工厂每天的加工生产成本为2.8万元，乙工厂每天的加工生产成本为2.4万元要使这批新产品的加工生产总成本不超过60万元，至少应安排甲工厂加工生产多少天？24. 如图，以AB为直径作半圆O，点C是半圆上一点，∠ABC的平分线交⊙O于E，D为BE延长线上一点，且DE＝FE.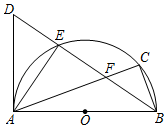
(1)、求证：AD为⊙O切线；(2)、若AB＝20，tan∠EBA＝ ，求BC的长.25. 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线OBCDA表示轿车离甲地距离y（千米）与时间x（小时）之间的函数关系.请根据图象解答下列问题：
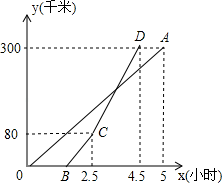(1)、当轿车刚到乙地时，此时货车距离乙地千米；(2)、当轿车与货车相遇时，求此时x的值；(3)、在两车行驶过程中，当轿车与货车相距20千米时，求x的值.26.
(1)、（操作发现）如图（1），在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝45°，连接AC，BD交于点M.
①AC与BD之间的数量关系为；
②∠AMB的度数为；
(2)、（类比探究）如图（2），在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC，交BD的延长线于点M.请计算 的值及∠AMB的度数；
(3)、（实际应用）如图（3），是一个由两个都含有30°角的大小不同的直角三角板ABC、DCE组成的图形，其中∠ACB＝∠DCE＝90°，∠A＝∠D＝30°且D、E、B在同一直线上，CE＝1，BC＝ ，求点A、D之间的距离.
27. 如图，二次函数y＝ax2﹣3ax+c的图象与x轴交于点A、B，与y轴交于点C直线y＝﹣x+4经过点B、C.
(1)、求抛物线的表达式；(2)、过点A的直线交抛物线于点M，交直线BC于点N.①点N位于x轴上方时，是否存在这样的点M，使得AM：NM＝5：3？若存在，求出点M的坐标；若不存在，请说明理由.
②连接AC，当直线AM与直线BC的夹角∠ANB等于∠ACB的2倍时，请求出点M的横坐标.