云南省2020年数学中考模拟试卷(3月)
试卷更新日期:2020-05-20 类型:中考模拟
一、填空题
-
1. 2020的相反数是.2. 因式分解:x2﹣4=.3. 如图,三角板直角顶点落在长方形纸片的一边上,∠1=35°,则∠2=°.
 4. 函数 的自变量x的取值范围是 .5. 如图,P是反比例函数y= 的图象第二象限上的一点,且矩形PEOF的面积为8,则k=.
4. 函数 的自变量x的取值范围是 .5. 如图,P是反比例函数y= 的图象第二象限上的一点,且矩形PEOF的面积为8,则k=.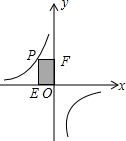 6. 如图,直线l为y= x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1 , 以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2 , 以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为().
6. 如图,直线l为y= x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1 , 以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2 , 以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为().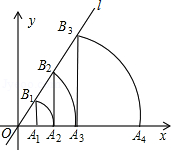
二、单选题
-
7. 下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )A、
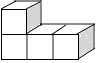 B、
B、 C、
C、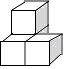 D、
D、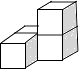 8. 贯彻落实党和政府扶贫开发方针、政策,负责组织实施和监督扶贫开发项目建设,开远市扶贫办2018年财政拨款收支总预算21800900元.将21800900用科学记数法表示为( )A、2.18009×108 B、0.218009×108 C、2.18009×107 D、21.8009×1069. 下列各式运算正确的是( )A、a2+a3=a5 B、a2•a3=a5 C、(ab2)3=ab6 D、a10÷a2=a510. 已知一个多边形的内角和为1080°,则这个多边形是( )A、九边形 B、八边形 C、七边形 D、六边形11. 关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( )
8. 贯彻落实党和政府扶贫开发方针、政策,负责组织实施和监督扶贫开发项目建设,开远市扶贫办2018年财政拨款收支总预算21800900元.将21800900用科学记数法表示为( )A、2.18009×108 B、0.218009×108 C、2.18009×107 D、21.8009×1069. 下列各式运算正确的是( )A、a2+a3=a5 B、a2•a3=a5 C、(ab2)3=ab6 D、a10÷a2=a510. 已知一个多边形的内角和为1080°,则这个多边形是( )A、九边形 B、八边形 C、七边形 D、六边形11. 关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( )
A、k≤﹣4 B、k<﹣4 C、k≤4 D、k<412.如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
 A、10cm B、16cm C、24cm D、26cm13. 某企业车间有50名工人,某一天他们生产的机器零件个数统计如表:
A、10cm B、16cm C、24cm D、26cm13. 某企业车间有50名工人,某一天他们生产的机器零件个数统计如表:零件个数(个)
6
7
8
人数(人)
15
22
10
表中表示零件个数的数据中,众数、中位数分别是( )
A、7个、7个 B、6个、7个 C、5个、6个 D、8个、6个14. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.
其中正确的个数是( )
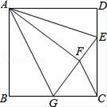 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5三、解答题
-
15. 计算:(﹣1)2﹣|﹣7|+ ×(2013﹣π)016. 点C是AE的中点,∠A=∠ECD,AB=CD,求证:△ABC≌△CDE.
 17. 某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,5个福娃2枚徽章145元,10个福娃3枚徽章280元(5个福娃为1套),则:(1)、一套“福娃”玩具和一枚徽章的价格各是多少元?(2)、买5套“福娃”玩具和10枚徽章共需要多少元?18. 九年级某班同学在“五四”游园活动中进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为A,B,C,随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.(1)、请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;(2)、规定当两次摸出的小球标号相同时中奖,求中奖的概率.19. 如图,在平行四边形ABCD中,E、F为对角线AC上两点,且AE=CF,请你从图中找出一对全等三角形,并给予证明.
17. 某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,5个福娃2枚徽章145元,10个福娃3枚徽章280元(5个福娃为1套),则:(1)、一套“福娃”玩具和一枚徽章的价格各是多少元?(2)、买5套“福娃”玩具和10枚徽章共需要多少元?18. 九年级某班同学在“五四”游园活动中进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为A,B,C,随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.(1)、请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;(2)、规定当两次摸出的小球标号相同时中奖,求中奖的概率.19. 如图,在平行四边形ABCD中,E、F为对角线AC上两点,且AE=CF,请你从图中找出一对全等三角形,并给予证明.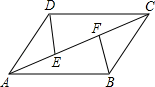 20. 某校组织了一次七年级科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品,C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
20. 某校组织了一次七年级科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品,C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.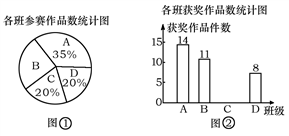 (1)、B班参赛作品有多少件?(2)、请你将图②的统计图补充完整;(3)、通过计算说明,哪个班的获奖率高?21. 某水果批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.(1)、现该商场要保证每天盈利6080元,同时又要顾客得到实惠,那么每千克应涨价多少元?(2)、若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?22. 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
(1)、B班参赛作品有多少件?(2)、请你将图②的统计图补充完整;(3)、通过计算说明,哪个班的获奖率高?21. 某水果批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.(1)、现该商场要保证每天盈利6080元,同时又要顾客得到实惠,那么每千克应涨价多少元?(2)、若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?22. 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.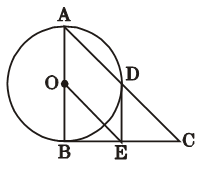 (1)、判断DE与⊙O的位置关系并说明理由;(2)、求证:(3)、若tanC= ,DE=2,求AD的长.23. 如图,抛物线y=﹣x2+2mx+m+2的图象与x轴交于A(﹣1,0),B两点,在x轴上方且平行于x轴的直线EF与抛物线交于E,F两点,E在F的左侧,过E,F分别作x轴的垂线,垂足是M,N.
(1)、判断DE与⊙O的位置关系并说明理由;(2)、求证:(3)、若tanC= ,DE=2,求AD的长.23. 如图,抛物线y=﹣x2+2mx+m+2的图象与x轴交于A(﹣1,0),B两点,在x轴上方且平行于x轴的直线EF与抛物线交于E,F两点,E在F的左侧,过E,F分别作x轴的垂线,垂足是M,N. (1)、求m的值及抛物线的顶点坐标;(2)、设BN=t,矩形EMNF的周长为C,求C与t的函数表达式;(3)、当矩形EMNF的周长为10时,将△ENM沿EN翻折,点M落在坐标平面内的点记为M',试判断点M'是否在抛物线上?并说明理由.
(1)、求m的值及抛物线的顶点坐标;(2)、设BN=t,矩形EMNF的周长为C,求C与t的函数表达式;(3)、当矩形EMNF的周长为10时,将△ENM沿EN翻折,点M落在坐标平面内的点记为M',试判断点M'是否在抛物线上?并说明理由.