西藏自治区2020年数学中考模拟试卷

试卷更新日期：2020-05-20 类型：中考模拟

进入出卷网下载

一、单选题

1. -2020的倒数是（）

A、2020 B、-2020 C、 $\frac{1}{2020}$ D、 $- \frac{1}{2020}$

查看试题解析
2. 下列计算结果等于x³的是（）

A、x⁶÷x² B、x⁴﹣x C、x+x² D、x²•x

查看试题解析
3. 若一个角为65°，则它的补角的度数为（）

A、25° B、35° C、115° D、125°

查看试题解析
4. 已知 $\frac{a}{2} = \frac{b}{3} (a \neq 0 ， b \neq 0)$ ，下列变形错误的是（）

A、 $\frac{a}{b} = \frac{2}{3}$ B、 $2 a = 3 b$ C、 $\frac{b}{a} = \frac{3}{2}$ D、 $3 a = 2 b$

查看试题解析
5. 若分式 $\frac{x^{2} - 4}{x}$ 的值为0，则x的值是（）

A、2或﹣2 B、2 C、﹣2 D、0

查看试题解析
6. 甲、乙、丙、丁四名同学在一次投掷实心球训练中，在相同条件下各投掷10次，他们成绩的平均数 $\bar{x}$ 与方差 $s^{2}$ 如下表：

甲
乙
丙
丁
平均数 $\bar{x}$ （米）
11.1
11.1
10.9
10.9
方差 $s^{2}$
1.1
1.2
1.3
1.4
若要选一名成绩好且发挥稳定的同学参加比赛，则应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 关于x的一元二次方程x²+4x+k=0有两个实数根，则k的取值范围是（）

A、k≤﹣4 B、k＜﹣4 C、k≤4 D、k＜4

查看试题解析
8. 如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF的位置，若四边形AECF的面积为25，DE=2，则AE的长为（）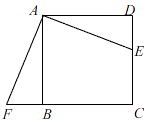

A、5 B、 $\sqrt{23}$ C、7 D、 $\sqrt{29}$

查看试题解析
9. 如图，⊙A过点O（0，0），C（ $\sqrt{3}$ ，0），D（0，1），点B是x轴下方⊙A上的一点，连接BO，BD，则∠OBD的度数是（）

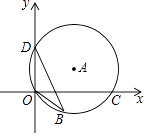A、15° B、30° C、45° D、60°

查看试题解析
10. 计算 $\frac{1}{2}$ + $\frac{1}{6}$ + $\frac{1}{12}$ + $\frac{1}{20}$ + $\frac{1}{30}$ +……+ $\frac{1}{9900}$ 的值为（）

A、 $\frac{1}{100}$ B、 $\frac{99}{100}$ C、 $\frac{1}{99}$ D、 $\frac{100}{99}$

查看试题解析
11. 我国古代数学著作《九章算术》卷七有下列问题：“今有共买物，人出八，盈三：人出七，不足四，问人数、物价几何？”意思是：现在有几个人共同出钱去买件物品，如果每人出8钱，则剩余3钱：如果每人出7钱，则差4钱．问有多少人，物品的价格是多少？设有x人，物品的价格为y元，可列方程（组）为（）

A、 ${\begin{matrix} 8 x - 3 = y \\ 7 x + 4 = y \end{matrix}$ B、 ${\begin{matrix} 8 x + 3 = y \\ 7 x - 4 = y \end{matrix}$ C、 $\frac{x + 3}{8} = \frac{x - 4}{7}$ D、 $\frac{y - 3}{8}$ = $\frac{y + 4}{7}$

查看试题解析
12. 如图是二次函数y=ax²+bx+c（a，b，c是常数，a≠0）图象的一部分，与x轴的交点A在点（2，0）和（3，0）之间，对称轴是x=1.对于下列说法：①ab＜0；②2a+b=0；③3a+c＞0；④当﹣1＜x＜3时，y＞0；其中正确的是（）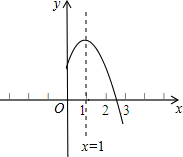

A、①② B、①②④ C、②③④ D、③④

查看试题解析

二、填空题

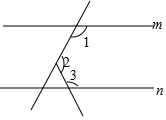
13. 分式方程 $\frac{3 x - 1}{x + 2}$ =4的解是x= ．

查看试题解析
14. 因式分解：a³－ab²＝.

查看试题解析
15. 如图，m∥n，∠1=110°，∠2=100°，则∠3=°.

查看试题解析
16. 已知圆锥的高h=4，底面半径r=3，则该圆锥侧面展开图的圆心角度数为°

查看试题解析
17. 小米的爸爸为了了解她的数学成绩情况，现从中随机抽取他的三次数学考试成绩，分别是87，93，90，则三次数学成绩的方差是．

查看试题解析
18. 如图，已知点A在反比例函数y= $\frac{k}{x}$ （x＞0）的图象上，作Rt△ABC，边BC在x轴上，点D为斜边AC的中点，连结DB并延长交y轴于点E，若△BCE的面积为4，则k=.

查看试题解析

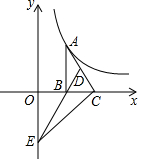
三、解答题

19. 计算： $\sqrt[3]{8} - 4 \cos 60^{0} - {(π - 3.14)}^{0} - {(\frac{1}{2})}^{- 1}$

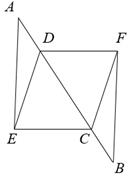
查看试题解析
20. 先化简，再求值： $(1 - \frac{1}{x}) \div \frac{x^{2} - 2 x + 1}{x}$ ，其中 $x = 2$ .

查看试题解析
21. 已知：如图，点A、D、C、B在同一条直线上，AD=BC，AE=BF，CE=DF；

(1)、求证：AE∥BF.

(2)、若EC=ED，请判断四边形ECFD的形状

查看试题解析
22. 学校准备购进一批甲、乙两种办公桌若干张，并且每买1张办公桌必须买2把椅子，椅子每把100元，若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元；购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.求甲、乙两种办公桌每张各多少元？

查看试题解析
23. 如图，有一铁塔AB，为了测量其高度，在水平面选取C，D两点，在点C处测得A的仰角为45°，距点C的10米D处测得A的仰角为60°，且C、D、B在同一水平直线上，求铁塔AB的高度（结果精确到0.1米， $\sqrt{3}$ ≈1.732）

查看试题解析
24. 如图，在三角形ABC中，AB=6，AC=BC=5，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF是⊙O的切线，D为切点，交CB的延长线于点E．

(1)、求证：DF⊥AC；

(2)、求tan∠E的值．

查看试题解析
25. 如图，已知抛物线经过点A（﹣1，0），B（4，0），C（0，2）三点，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P做x轴的垂线l交抛物线于点Q，交直线BD于点M.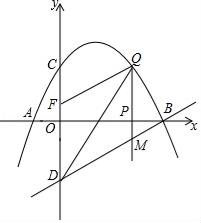

(1)、求该抛物线所表示的二次函数的表达式；

(2)、已知点F（0， $\frac{1}{2}$ ），当点P在x轴上运动时，试求m为何值时，四边形DMQF是平行四边形？

(3)、点P在线段AB运动过程中，是否存在点Q，使得以点B、Q、M为顶点的三角形与△BOD相似？若存在，求出点Q的坐标；若不存在，请说明理由.

查看试题解析

	甲	乙	丙	丁
平均数 $\bar{x}$ （米）	11.1	11.1	10.9	10.9
方差 $s^{2}$	1.1	1.2	1.3	1.4