黑龙江省集贤县2017-2018学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-20 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 × =4 B、 + = C、 ÷ =2 D、 =﹣152. 一次函数 的图象经过原点,则k的值为A、2 B、 C、2或 D、33. 在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数4. 关于一次函数y=﹣2x+3,下列结论正确的是( )A、图象过点(1,﹣1) B、图象经过一、二、三象限 C、y随x的增大而增大 D、当x> 时,y<05. 如图,点O为四边形ABCD内任意一点,E,F,G,H分别为OA,OB,OC,OD的中点,则四边形EFGH的周长为( )
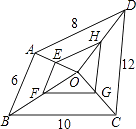 A、9 B、12 C、18 D、不能确定6. 如图,平行四边形ABCD的两条对角线相交于点O,点E是AB边的中点,图中已有三角形与△ADE面积相等的三角形(不包括△ADE)共有( )个.
A、9 B、12 C、18 D、不能确定6. 如图,平行四边形ABCD的两条对角线相交于点O,点E是AB边的中点,图中已有三角形与△ADE面积相等的三角形(不包括△ADE)共有( )个.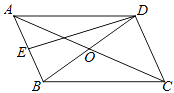 A、3 B、4 C、5 D、67. 甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )
A、3 B、4 C、5 D、67. 甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )甲
乙
丙
丁
平均数
80
85
85
80
方 差
42
42
54
59
A、甲 B、乙 C、丙 D、丁8. 如图,平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE等于( )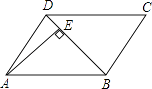 A、20° B、25° C、30° D、35°9. 如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
A、20° B、25° C、30° D、35°9. 如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )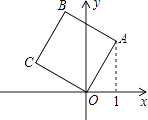 A、(﹣2,1) B、(﹣1,2) C、( ,﹣1) D、(﹣ ,1)10. 我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
A、(﹣2,1) B、(﹣1,2) C、( ,﹣1) D、(﹣ ,1)10. 我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.
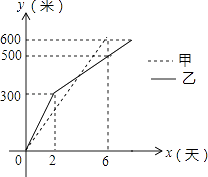 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 若最简二次根式 与 的被开方数相同,则a的值为.12. 化简: 的结果是.13. 在两条垂直相交的道路上,一辆自行车和一辆摩托车相遇后又分别向北向东驶去,若自行车与摩托车每秒分别行驶7.5米、10米,则10秒后两车相距米;14. 若等腰三角形中相等的两边长为10cm,第三边长为16cm,那么第三边上的高为cm.15. 平行四边形ABCD中,∠A-∠B=20°,则∠A= , ∠B=.16. 在函数y= 中,自变量x的取值范围是 .17.
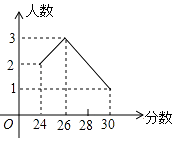
在2017年的理化生实验考试中某校6名学生的实验成绩统计如图,这组数据的众数是分.
 18. 如图,小华将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为 .
18. 如图,小华将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为 .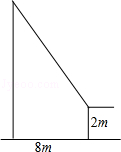 19. 如图所示,线段EF过平行四边形ABCD的对角线的交点O,交AD于点E,交BC于点F。已知AB=4,BC=5,EF=3,那么四边形EFCD的周长是.
19. 如图所示,线段EF过平行四边形ABCD的对角线的交点O,交AD于点E,交BC于点F。已知AB=4,BC=5,EF=3,那么四边形EFCD的周长是.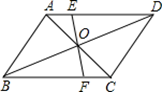 20. 如图,直线y= 与y= x交于A(3,1)与x轴交于B(6,0),则不等式组0 的解集为 .
20. 如图,直线y= 与y= x交于A(3,1)与x轴交于B(6,0),则不等式组0 的解集为 .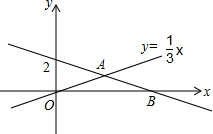
三、综合题
-
21. 计算(1)、 ;(2)、 ÷22. 为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:
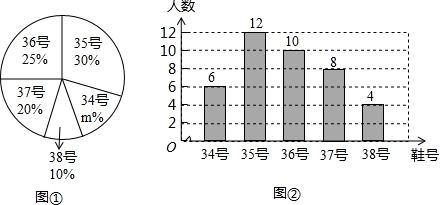 (1)、本次接受随机抽样调查的学生人数为 , 图①中 的值为;(2)、本次调查获取的样本数据的众数为 , 中位数为;(3)、根据样本数据,若学校计划购买 双运动鞋,建议购买 号运动鞋双.23. 如图,有一个直角三角形纸片,两直角边 cm, cm,现将直角边沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
(1)、本次接受随机抽样调查的学生人数为 , 图①中 的值为;(2)、本次调查获取的样本数据的众数为 , 中位数为;(3)、根据样本数据,若学校计划购买 双运动鞋,建议购买 号运动鞋双.23. 如图,有一个直角三角形纸片,两直角边 cm, cm,现将直角边沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗? 24. 已知,如图,在△ABC中,BD是∠ABC的平分线,DE∥BC交AB于E,EF∥AC交BC于F,请判断BE与FC的数量关系,并说明理由。
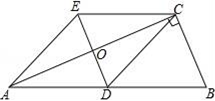
24. 已知,如图,在△ABC中,BD是∠ABC的平分线,DE∥BC交AB于E,EF∥AC交BC于F,请判断BE与FC的数量关系,并说明理由。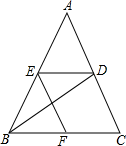 25. 如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
25. 如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.求证:四边形ADCE是菱形.
 26. 如图,直线l1的函数表达式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C.
26. 如图,直线l1的函数表达式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C.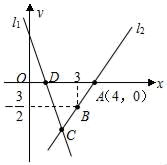 (1)、求点D的坐标;(2)、求直线l2的解析表达式;(3)、求△ADC的面积.27. 某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
(1)、求点D的坐标;(2)、求直线l2的解析表达式;(3)、求△ADC的面积.27. 某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题: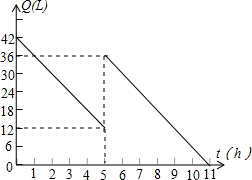 (1)、机动车行驶几小时后加油?加了多少油?(2)、请求出加油前油箱余油量Q与行驶时间t之间的关系式;(3)、如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.28. 如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)、机动车行驶几小时后加油?加了多少油?(2)、请求出加油前油箱余油量Q与行驶时间t之间的关系式;(3)、如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.28. 如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.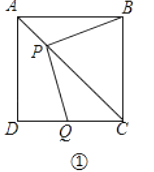
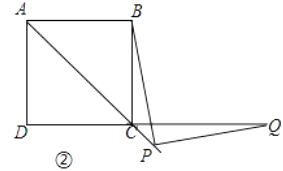 (1)、如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;(2)、如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
(1)、如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;(2)、如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.