黑龙江省哈尔滨市香坊区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-20 类型:期末考试
一、单选题
-
1. 下列关于x的方程是一元二次方程的是( )A、 B、 C、 D、2. 下列图形中,不是轴对称图形的是( )A、矩形 B、菱形 C、平行四边形 D、正方形3. 若直角三角形的两条直角边的长分别为 、 ,则斜边上的高为( )A、 B、 C、 D、4. 下列说法不正确的是( )A、两组对边分别相等的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、对角线互相平分且垂直的四边形是菱形 D、一个角是直角的四边形是矩形5. 关于 的一元二次方程 有两个不相等的实数根,那么 的取值范围是( )A、 B、 且 C、 且 D、6. 直线 沿 轴向右平移2个单位长度,得到的图象对应的函数解析式为( )A、 B、 C、 D、7. 如图,四边形 中, , , ,连接 , , ,则 的长为( )
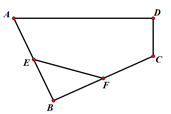 A、 B、 C、 D、8. 如图,小元要在一幅长 、宽 的风景面的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂图,使风景画的面积占整个挂图面积的54%,设金色纸边的宽为 ,根据题意可列方程( )
A、 B、 C、 D、8. 如图,小元要在一幅长 、宽 的风景面的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂图,使风景画的面积占整个挂图面积的54%,设金色纸边的宽为 ,根据题意可列方程( ) A、 B、 C、 D、9. 如图,矩形纸片 , ,将其折叠使点 与点 重合,点 的对应点为点 ,折痕为 ,那么 和 的长分别为( )
A、 B、 C、 D、9. 如图,矩形纸片 , ,将其折叠使点 与点 重合,点 的对应点为点 ,折痕为 ,那么 和 的长分别为( )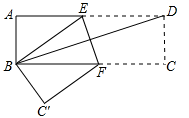 A、4和 B、4和 C、5和 D、5和10. 甲、乙两名运动员同时从 地出发前往 地,在笔直的公路上进行骑自行车训练如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程 (千米)与行驶时间 (小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时, 或 .其中正确的个数有( )
A、4和 B、4和 C、5和 D、5和10. 甲、乙两名运动员同时从 地出发前往 地,在笔直的公路上进行骑自行车训练如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程 (千米)与行驶时间 (小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时, 或 .其中正确的个数有( )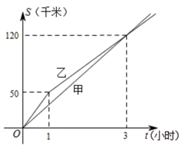 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 函数 中,自变量x的取值范围为 .12. 关于 的一元二次方程 有一个根为0,则 的值为 .13. 已知菱形 的边长为4, ,则菱形 的面积为 .14. 若 , ,则 = .15. 如图,平行四边形 中, 平分 ,交 于点F, ,交 点 , ,则 = .
 16. 如图,在正方形 的右侧作等边三角形 ,分别连接 交于点 ,连接 ,则 .
16. 如图,在正方形 的右侧作等边三角形 ,分别连接 交于点 ,连接 ,则 . 17. 在平面直角坐标系中,一次函数 的图象与 轴交于点 ,与 轴交于点 , 长为5,则 的值为 .18. 某品牌运动服原来每件售价640元,经过两次降价,售价降低了280元,已知两次降价的百分率相同,则每次降价的百分率为 .19. 如图,函数 和 的图象交于点 ,根据图象可知,关于 的不等式 的解集为 .
17. 在平面直角坐标系中,一次函数 的图象与 轴交于点 ,与 轴交于点 , 长为5,则 的值为 .18. 某品牌运动服原来每件售价640元,经过两次降价,售价降低了280元,已知两次降价的百分率相同,则每次降价的百分率为 .19. 如图,函数 和 的图象交于点 ,根据图象可知,关于 的不等式 的解集为 . 20. 如图,矩形 中, ,延长 交 于点 ,延长 交 于点 ,过点 作 ,交 的延长线于点 , ,则 = .
20. 如图,矩形 中, ,延长 交 于点 ,延长 交 于点 ,过点 作 ,交 的延长线于点 , ,则 = .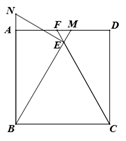
三、综合题
-
21. 计算(1)、(2)、22. 如图所示,图1、图2分别是 的网格,网格中的每个小正方形的边长均为1.请按下列要求分别画出相应的图形,且所画图形的每个顶点均在所给小正方形的顶点上.
 (1)、在图1中画出一个周长为 的菱形 (非正方形);(2)、在图2中画出一个面积为9的平行四边形 ,且满足 ,请直接写出平行四边形 的周长.23. 如图,在平面直角坐标系中,直线 的解析式为 ,点 的坐标分别为(1,0),(0,2),直线 与直线 相交于点 .
(1)、在图1中画出一个周长为 的菱形 (非正方形);(2)、在图2中画出一个面积为9的平行四边形 ,且满足 ,请直接写出平行四边形 的周长.23. 如图,在平面直角坐标系中,直线 的解析式为 ,点 的坐标分别为(1,0),(0,2),直线 与直线 相交于点 .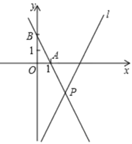 (1)、求直线 的解析式;(2)、点 在第一象限的直线 上,连接 ,且 ,求点 的坐标.24. 已知四边形 是菱形,点 分别在 上,且 ,点 分别在 上, 与 相交于点 .
(1)、求直线 的解析式;(2)、点 在第一象限的直线 上,连接 ,且 ,求点 的坐标.24. 已知四边形 是菱形,点 分别在 上,且 ,点 分别在 上, 与 相交于点 . (1)、如图1,求证:四边形 是菱形;(2)、如图2,连接 ,在不添加任何辅助线的情况下,请直接写出面积相等的四边形25. 益民商店经销某种商品,进价为每件80元,商店销售该商品每件售价高干8元且不超过120元若售价定为每件120元时,每天可销售200件,市场调查反映:该商品售价在120元的基础上,每降价1元,每天可多销售10件,设该商品的售价为 元,每天销售该商品的数量为 件.(1)、求y与x之间的函数关系式;(2)、商店在销售该商品时,除成本外每天还需支付其余各种费用1000元,益民商店在某一天销售该商品时共获利8000元,求这一天该商品的售价为多少元?26. 已知四边形 中, ,垂足为点 , .
(1)、如图1,求证:四边形 是菱形;(2)、如图2,连接 ,在不添加任何辅助线的情况下,请直接写出面积相等的四边形25. 益民商店经销某种商品,进价为每件80元,商店销售该商品每件售价高干8元且不超过120元若售价定为每件120元时,每天可销售200件,市场调查反映:该商品售价在120元的基础上,每降价1元,每天可多销售10件,设该商品的售价为 元,每天销售该商品的数量为 件.(1)、求y与x之间的函数关系式;(2)、商店在销售该商品时,除成本外每天还需支付其余各种费用1000元,益民商店在某一天销售该商品时共获利8000元,求这一天该商品的售价为多少元?26. 已知四边形 中, ,垂足为点 , . (1)、如图1,求证: ;(2)、如图2,点 为 上一点,连接 , ,求证: ;(3)、在(2)的条件下,如图3,点 为 上一点,连接 ,点 为 的中点,分别连接 , , + = = , ,求线段 的长.27. 在平面直角坐标系中,一次函数 的图象与 轴负半轴交于点 ,与 轴正半轴交于点 ,点 为直线 上一点, ,点 为 轴正半轴上一点,连接 , 的面积为48.
(1)、如图1,求证: ;(2)、如图2,点 为 上一点,连接 , ,求证: ;(3)、在(2)的条件下,如图3,点 为 上一点,连接 ,点 为 的中点,分别连接 , , + = = , ,求线段 的长.27. 在平面直角坐标系中,一次函数 的图象与 轴负半轴交于点 ,与 轴正半轴交于点 ,点 为直线 上一点, ,点 为 轴正半轴上一点,连接 , 的面积为48. (1)、如图1,求点 的坐标;(2)、如图2,点 分别在线段 上,连接 ,点 的横坐标为 ,点 的横坐标为 ,求 与 的函数关系式(不要求写出自变量 的取值范围);(3)、在(2)的条件下,如图3,连接 ,点 为 轴正半轴上点 右侧一点,点 为第一象限内一点, , ,延长 交 于点 ,点 为 上一点,直线 经过点 和点 ,过点 作 ,交直线 于点 ,连接 ,请你判断四边形 的形状,并说明理由.
(1)、如图1,求点 的坐标;(2)、如图2,点 分别在线段 上,连接 ,点 的横坐标为 ,点 的横坐标为 ,求 与 的函数关系式(不要求写出自变量 的取值范围);(3)、在(2)的条件下,如图3,连接 ,点 为 轴正半轴上点 右侧一点,点 为第一象限内一点, , ,延长 交 于点 ,点 为 上一点,直线 经过点 和点 ,过点 作 ,交直线 于点 ,连接 ,请你判断四边形 的形状,并说明理由.