陕西省2020年数学中考模拟试卷(4月)
试卷更新日期:2020-05-20 类型:中考模拟
一、单选题
-
1. ﹣4的倒数是( )A、 B、﹣ C、4 D、﹣4
-
2. 如图的几何体是由五个小正方体组合而成的,则这个几何体的左视图是( )
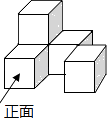 A、
A、 B、
B、 C、
C、 D、
D、
-
3. 下列计算中,正确的是( )A、x3•x2=x4 B、x(x-2)=-2x+x2 C、(x+y)(x-y)=x2+y2 D、3x3y2÷xy2=3x4
-
4. 如图,AB∥CD,CE交AB于点F.∠A=20°,∠E=30°,则∠C的度数为( )
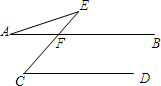 A、50° B、55° C、60° D、65°
A、50° B、55° C、60° D、65° -
5. 点A(x1 , y1)、B(x2 , y2)都在直线y=kx+2(k<0)上,且x1<x2则y1、y2的大小关系是( )A、y1 =y2 B、y1 <y2 C、y1 >y2 D、y1 ≥y2
-
6.
如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则的值等于( )
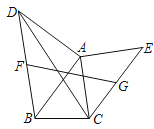 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 已知直线y=mx﹣3与直线y=x+3m,当﹣2≤x<2时,两直线有交点,则m的取值范围是( )A、m<﹣ 或m>﹣5 B、﹣5≤m≤﹣ C、﹣5<m D、m=﹣
-
8. 如图,在Rt△ABC中,∠B=45°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
 A、①②③ B、②③④ C、①②④ D、①②③④
A、①②③ B、②③④ C、①②④ D、①②③④ -
9. 如图,半径为5的⊙O中,CD是⊙O的直径,弦AB⊥CD于E,AB=8,F是 上一点,连接AF,DF,则tan∠F的值为( )
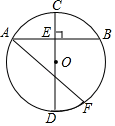 A、 B、 C、 D、2
A、 B、 C、 D、2 -
10. 对于二次函数y=4(x+1)(x﹣3)下列说法正确的是( )A、图象开口向下 B、与x轴交点坐标是(1,0)和(﹣3,0) C、x<0时,y随x的增大而减小 D、图象的对称轴是直线x=﹣1
二、填空题
-
11. 在实数 , ,0, ,2π中,无理数有.
-
12. 若正六边形的边长为3,则其面积为.
-
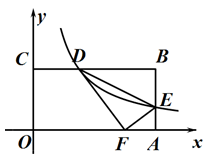
13. 如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点B的坐标为(12,6),反比例函数 的图象分别交边BC、AB于点D、E,连结DE,ΔDEF与ΔDEB关于直线DE对称.当点F正好落在边OA上时,则k的值为 .
-
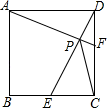
14. 如图,正方形ABCD的边长为4,点E、F分别是BC,CD边上的动点,且CE+CF=4,DE和AF相交于点P,在点E,F运动的过程中,CP的最小值为.
三、解答题
-
15. 计算:
-
16. 计算:(1)、 ;(2)、 .
-
17. 菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,动点P在线段AC上从点A向点C以4个单位/秒的速度运动,过点P作EF⊥AC,交菱形ABCD的边于点E、F,在直线AC上有一点G,使△AEF与△GEF关于EF对称.设菱形ABCD被四边形AEGF盖住部分的面积为S1 , 未被盖住部分的面积为S2 , 点P运动时间为x秒.
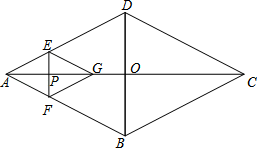 (1)、用含x的代数式分别表示S1 , S2;(2)、若S1=S2 , 求x的值.
(1)、用含x的代数式分别表示S1 , S2;(2)、若S1=S2 , 求x的值. -
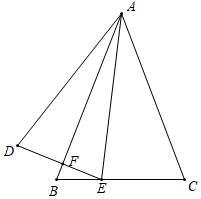
18. 如图,点E是△ABC的BC边上的一点,∠AEC=∠AED,ED=EC,∠D=∠B,求证:AB=AC.
-
19. 我校八年级有800名学生,在体育中考前进行一次排球模拟测试,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:
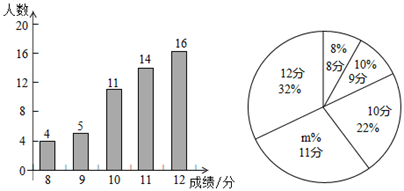 (1)、本次抽取到的学生人数为 , 图2中 的值为.(2)、本次调查获取的样本数据的平均数是 , 众数是 , 中位数是.(3)、根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
(1)、本次抽取到的学生人数为 , 图2中 的值为.(2)、本次调查获取的样本数据的平均数是 , 众数是 , 中位数是.(3)、根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人? -
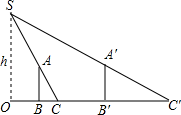
20. 为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
-
21. 某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.(1)、求每部A型手机和B型手机的销售利润分别为多少元?(2)、该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)、实际进货时,厂家对B型手机出厂价下调m(30<m<100)元,且限定商店最多购进B型手机80台.若商店保持两种手机的售价不变,请你根据以上信息及(2)中的条件,设计出使这110部手机销售总利润最大的进货方案. -
22. 在“阳光体育”活动时间,小英、小丽、小敏、小洁四位同学进行一次羽毛球单打比赛,要从中选出两位同学打第一场比赛
(1)、若已确定小英打第一场,再从其余三位同学中随机选取一位,求恰好选中小丽同学的概率(2)、用画树状图或列表的方法,求恰好选中小敏、小洁两位同学进行比赛的概率 -
23. 如图,AB=AC,⊙O为△ABC的外接圆,AF为⊙O的直径,四边形ABCD是平行四边形.
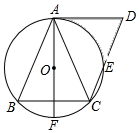 (1)、求证:AD是⊙O的切线;(2)、若∠BAC=45°,AF=2,求阴影部分的面积.
(1)、求证:AD是⊙O的切线;(2)、若∠BAC=45°,AF=2,求阴影部分的面积. -
24. 如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.
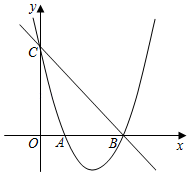 (1)、求此抛物线的解析式;(2)、若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.
(1)、求此抛物线的解析式;(2)、若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.①用含m的代数式表示线段PD的长.
②连接PB,PC,求△PBC的面积最大时点P的坐标.
(3)、设抛物线的对称轴与BC交于点E,点M是抛物线的对称轴上一点,N为y轴上一点,是否存在这样的点M和点N,使得以点C、E、M、N为顶点的四边形是菱形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由. -
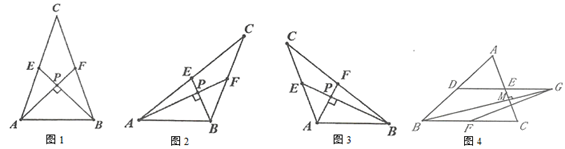
25. 某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中, 、 是 的中线, 于点 ,像 这样的三角形均称为“中垂三角形”.
 (1)、(特例探究)
(1)、(特例探究)如图1,当 , 时, , ;
如图2,当 , 时, , ;
(2)、(归纳证明)请你观察(1)中的计算结果,猜想 、 、 三者之间的关系,用等式表示出来,并利用图3证明你的结论;
(3)、(拓展证明)如图4,在 中, , , 、 、 分别是边 、 的中点,连结 并延长至 ,使得 ,连结 ,当 于点 时,求 的长.
