辽宁省沈阳市2020年数学中考一模试卷
试卷更新日期:2020-05-20 类型:中考模拟
一、单选题
-
1. 下列4个数: , ,π,( )0 , 其中无理数是( )A、 B、 C、π D、( )02. 如图是由6个大小相同的小正方体搭成的几何体,这个几何体的左视图是( )
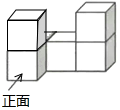 A、
A、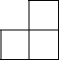 B、
B、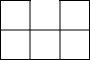 C、
C、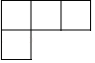 D、
D、 3. 下列计算正确的是( )A、2 ﹣4 =﹣2 B、3a+a=3 C、3a•a=3 D、4 ÷2 =24. 已知一天有86400秒,一年按365天计算共有31536000秒,用科学记数法表示31536000正确的是( )A、 B、 C、 D、5. 如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )
3. 下列计算正确的是( )A、2 ﹣4 =﹣2 B、3a+a=3 C、3a•a=3 D、4 ÷2 =24. 已知一天有86400秒,一年按365天计算共有31536000秒,用科学记数法表示31536000正确的是( )A、 B、 C、 D、5. 如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )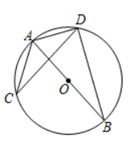 A、 B、 C、 D、6. 如图,矩形 的顶点 , 在反比例函数 的图象上,若点 的坐标为 , , 轴,则点 的坐标为( )
A、 B、 C、 D、6. 如图,矩形 的顶点 , 在反比例函数 的图象上,若点 的坐标为 , , 轴,则点 的坐标为( )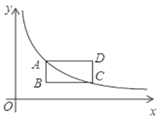 A、 B、 C、 D、7. 某工厂计划生产300个零件,由于采用新技术,实际每天生产零件的数量是原计划的2倍,因此提前5天完成任务.设原计划每天生产零件x个,根据题意,所列方程正确的是( )A、 ﹣ =5 B、 ﹣ =5 C、 ﹣ =5 D、 ﹣ =58. 如图,在距离铁轨200米处的 处,观察由南宁开往百色的“和谐号”动车,当动车车头在 处时,恰好位于 处的北偏东 方向上,10秒钟后,动车车头到达 处,恰好位于 处西北方向上,则这时段动车的平均速度是( )米/秒.
A、 B、 C、 D、7. 某工厂计划生产300个零件,由于采用新技术,实际每天生产零件的数量是原计划的2倍,因此提前5天完成任务.设原计划每天生产零件x个,根据题意,所列方程正确的是( )A、 ﹣ =5 B、 ﹣ =5 C、 ﹣ =5 D、 ﹣ =58. 如图,在距离铁轨200米处的 处,观察由南宁开往百色的“和谐号”动车,当动车车头在 处时,恰好位于 处的北偏东 方向上,10秒钟后,动车车头到达 处,恰好位于 处西北方向上,则这时段动车的平均速度是( )米/秒. A、 B、 C、200 D、3009. 如图,ABCDEF为⊙O的内接正六边形,AB=a,则图中阴影部分的面积是( )
A、 B、 C、200 D、3009. 如图,ABCDEF为⊙O的内接正六边形,AB=a,则图中阴影部分的面积是( ) A、 B、 C、 D、10. 为了配合 “我读书,我快乐”读书节活动,某书店推出一种优惠卡,每张卡售价20元,凭卡购书可享受8折优惠,小慧同学到该书店购书,她先买优惠卡再凭卡付款,结果节省了10元,若此次小慧同学不买卡直接购书,则她需付款( )A、140元 B、150元 C、160元 D、200元
A、 B、 C、 D、10. 为了配合 “我读书,我快乐”读书节活动,某书店推出一种优惠卡,每张卡售价20元,凭卡购书可享受8折优惠,小慧同学到该书店购书,她先买优惠卡再凭卡付款,结果节省了10元,若此次小慧同学不买卡直接购书,则她需付款( )A、140元 B、150元 C、160元 D、200元二、填空题
-
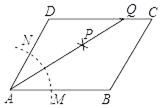
11. 若分式 的值为0,则x的值为 .12. 在某一时刻,测得一根高为 的竹竿的影长为 ,同时同地测得一栋楼的影长为 ,则这栋楼的高度为 .13. 不等式组 的解集是.14. 如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于 MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为.
 15. 一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从A村、B村同时出发前往C村,甲乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B两村相距10km;②出发1.25h后两人相遇:③甲每小时比乙多骑行8km;④相遇后,乙又骑行了15min时两人相距2km.其中正确的有.(填序号)
15. 一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从A村、B村同时出发前往C村,甲乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B两村相距10km;②出发1.25h后两人相遇:③甲每小时比乙多骑行8km;④相遇后,乙又骑行了15min时两人相距2km.其中正确的有.(填序号)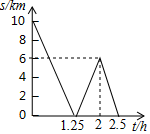 16. 如图, 是等边三角形,点D为BC边上一点, ,以点D为顶点作正方形DEFG,且 ,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为.
16. 如图, 是等边三角形,点D为BC边上一点, ,以点D为顶点作正方形DEFG,且 ,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为.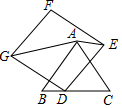
三、解答题
-
17. 计算: .18. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.19. 如图,将平行四边形纸片 沿一条直线折叠,使点 与点 重合,点 落在点 处,折痕为 .求证:
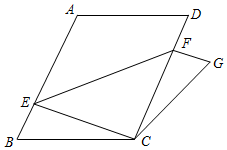 (1)、 ;(2)、 .20. “勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
(1)、 ;(2)、 .20. “勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图: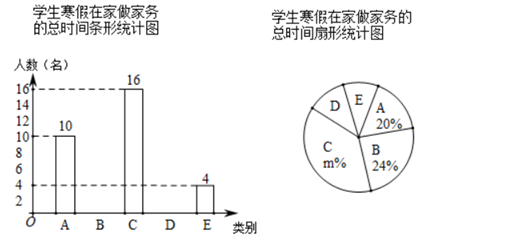
根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生;(2)、请根据以上信息直接在答题卡中补全条形统计图;(3)、扇形统计图中m的值是 , 类别D所对应的扇形圆心角的度数是度;(4)、若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.21. 某超市用1200元购进一批甲玩具,用800元购进一批乙玩具,所购甲玩具件数是乙玩具件数的 ,已知甲玩具的进货单价比乙玩具的进货单价多1元.(1)、求:甲、乙玩具的进货单价各是多少元?(2)、玩具售完后,超市决定再次购进甲、乙玩具(甲、乙玩具的进货单价不变),购进乙玩具的件数比甲玩具件数的2倍多60件,求:该超市用不超过2100元最多可以采购甲玩具多少件?22. 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G. (1)、试判断FG与⊙O的位置关系,并说明理由.(2)、若AC=3,CD=2.5,求FG的长.23. 如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为每秒1个单位,过点P作PE⊥AO交AB于点E,一点到达,另一点即停.设点P的运动时间为t秒(t>0).
(1)、试判断FG与⊙O的位置关系,并说明理由.(2)、若AC=3,CD=2.5,求FG的长.23. 如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为每秒1个单位,过点P作PE⊥AO交AB于点E,一点到达,另一点即停.设点P的运动时间为t秒(t>0).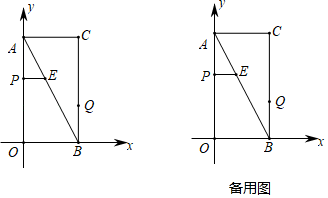 (1)、填空:用含t的代数式表示下列各式:AP= , CQ=.(2)、①当PE= 时,求点Q到直线PE的距离.
(1)、填空:用含t的代数式表示下列各式:AP= , CQ=.(2)、①当PE= 时,求点Q到直线PE的距离.②当点Q到直线PE的距离等于 时,直接写出t的值.
(3)、在动点P、Q运动的过程中,点H是矩形AOBC(包括边界)内一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出点H的横坐标.24. 如图,在△ABC中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.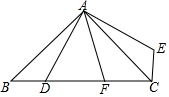 (1)、求证:△ABD≌△ACE;(2)、若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;(3)、在(2)的条件下,若BD=3,CF=4,求AD的长.25. 如图,抛物线 交 轴于点 和点 ,交 轴于点 .已知点 的坐标为 ,点 为第二象限内抛物线上的一个动点,连接 、 、 .
(1)、求证:△ABD≌△ACE;(2)、若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;(3)、在(2)的条件下,若BD=3,CF=4,求AD的长.25. 如图,抛物线 交 轴于点 和点 ,交 轴于点 .已知点 的坐标为 ,点 为第二象限内抛物线上的一个动点,连接 、 、 .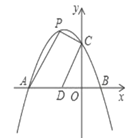
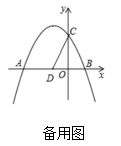 (1)、求这个抛物线的表达式.(2)、当四边形 面积等于4时,求点 的坐标.(3)、①点 在平面内,当 是以 为斜边的等腰直角三角形时,直接写出满足条件的所有点 的坐标;
(1)、求这个抛物线的表达式.(2)、当四边形 面积等于4时,求点 的坐标.(3)、①点 在平面内,当 是以 为斜边的等腰直角三角形时,直接写出满足条件的所有点 的坐标;②在①的条件下,点 在抛物线对称轴上,当 时,直接写出满足条件的所有点 的坐标.