辽宁省沈阳2020年数学中考模拟试卷(一)
试卷更新日期:2020-05-20 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、2 C、 D、2. 如图是由6个棱长均为1的正方体组成的几何体,从左面看到的该几何体的形状为( )
 A、
A、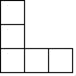 B、
B、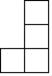 C、
C、 D、
D、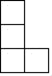 3. 人体中红细胞的直径约为0.0000077 m,用科学记数法表示数的结果是( )
3. 人体中红细胞的直径约为0.0000077 m,用科学记数法表示数的结果是( )
A、0.77×10-5 m B、0.77×10-6 m C、7.7×10-5 m D、7.7×10-6 m4. 下列计算中正确的是( )A、b3•b2=b6 B、x3+x3=x6 C、a2÷a2=0 D、(﹣a3)2=a65. 已知关于x的一元二次方程x2﹣m=2x有两个不相等的实数根,则m的取值范围是( )A、m>0 B、m>﹣1 C、m<0 D、m<﹣16. 已知一组数据2,3,4,x,1,4,3有唯一的众数4,则这组数据的中位数是( )A、2 B、3 C、4 D、57. 从一副完整的扑克牌中任意抽取1张,下列事件与抽到“K”的概率相同的是( )A、抽到“大王” B、抽到“2” C、抽到“小王” D、抽到“红桃”8. 正六边形的周长为12,则它的面积为( )A、 B、 C、 D、9. 如图,AC=AD,BC=BD,则有( ) A、AB垂直平分CD B、CD垂直平分AB C、AB与CD互相垂直平分 D、CD平分∠ACB10. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,c<﹣1,其对称轴为直线x=﹣1,与x轴的交点为(x1 , 0)、(x2 , 0),其中0<x1<1,有下列结论:①abc>0;②﹣3<x2<﹣2;③4a﹣2b+c<﹣1;④a﹣b>am2+bm(m≠﹣1);其中,正确的结论个数是( )
A、AB垂直平分CD B、CD垂直平分AB C、AB与CD互相垂直平分 D、CD平分∠ACB10. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,c<﹣1,其对称轴为直线x=﹣1,与x轴的交点为(x1 , 0)、(x2 , 0),其中0<x1<1,有下列结论:①abc>0;②﹣3<x2<﹣2;③4a﹣2b+c<﹣1;④a﹣b>am2+bm(m≠﹣1);其中,正确的结论个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 分解因式6xy2-9x2y-y3 = .12. 已知反比例函数y= 在每个象限内y随x增大而减小,则m的取值范围是.13. 若不等式组 的解集是﹣1<x≤1,则a= , b= .14. 如图,四边形ABCD内接于⊙O,OC∥AD,∠DAB=60°,∠ADC=106°,则∠OCB=°.
 15. 一男生推铅球,铅球行进高度y与水平距离x之间的关系是 ,则铅球推出的距离是.此时铅球行进高度是.16. 如图,矩形ABCD中,AD=4,AB=2.点E是AB的中点,点F是BC边上的任意一点(不与B、C重合),△EBF沿EF翻折,点B落在B'处,当DB'的长度最小时,BF的长度为.
15. 一男生推铅球,铅球行进高度y与水平距离x之间的关系是 ,则铅球推出的距离是.此时铅球行进高度是.16. 如图,矩形ABCD中,AD=4,AB=2.点E是AB的中点,点F是BC边上的任意一点(不与B、C重合),△EBF沿EF翻折,点B落在B'处,当DB'的长度最小时,BF的长度为.
三、解答题
-
17. 计算:18. 如图, ABCD中,点E是BC边的一点,延长AD至点F,使∠DFC=∠DEC.
求证:四边形DECF是平行四边形.
 19. 中雅培粹学校举办运动会,全校有3000名同学报名参加校运会,为了解各类运动赛事的分布情况,从中抽取了部分同学进行统计:A.田径类,B.球类,C.团体类,D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.
19. 中雅培粹学校举办运动会,全校有3000名同学报名参加校运会,为了解各类运动赛事的分布情况,从中抽取了部分同学进行统计:A.田径类,B.球类,C.团体类,D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图. (1)、这次统计共抽取了位同学,扇形统计图中的 , 的度数是;(2)、请将条形统计图补充完整;(3)、估计全校共多少学生参加了球类运动.20. 一个不透明的袋子中装有3个标号分别为1、2、3的完全相同的小球,随机地摸出一个小球不放回,再随机地摸出一个小球.(1)、采用树状图或列表法列出两次摸出小球出现的所有可能结果;(2)、求摸出的两个小球号码之和等于4的概率.21. 吉祥超市准备购进甲、乙两种绿色袋装食品共800袋.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)、这次统计共抽取了位同学,扇形统计图中的 , 的度数是;(2)、请将条形统计图补充完整;(3)、估计全校共多少学生参加了球类运动.20. 一个不透明的袋子中装有3个标号分别为1、2、3的完全相同的小球,随机地摸出一个小球不放回,再随机地摸出一个小球.(1)、采用树状图或列表法列出两次摸出小球出现的所有可能结果;(2)、求摸出的两个小球号码之和等于4的概率.21. 吉祥超市准备购进甲、乙两种绿色袋装食品共800袋.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.甲
乙
进价(元/袋)
m
m﹣2
售价(元/袋)
20
13
(1)、求m的值;(2)、假如购进的甲、乙两种绿色袋装食品全部卖出,所获总利润不少于5200元,且不超过5280元,问该超市有几种进货方案?(利润=售价﹣进价)22. 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC的延长线于点E,交AB的延长线于点F.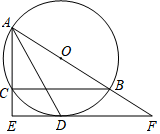 (1)、求证:EF是⊙O的切线;(2)、若AC=8,CE=4,求弧BD的长.(结果保留π)23. 在平面直角坐标系中,一次函数y=﹣ x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.
(1)、求证:EF是⊙O的切线;(2)、若AC=8,CE=4,求弧BD的长.(结果保留π)23. 在平面直角坐标系中,一次函数y=﹣ x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P. (1)、求点A、B的坐标;(2)、若OP=PA,求k的值;(3)、在(2)的条件下,C是线段BP上一点,CE⊥x轴于E,交OP于D,若CD=2ED,求C点的坐标.24. 如图将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°)得到正方形AB′C′D′.
(1)、求点A、B的坐标;(2)、若OP=PA,求k的值;(3)、在(2)的条件下,C是线段BP上一点,CE⊥x轴于E,交OP于D,若CD=2ED,求C点的坐标.24. 如图将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°)得到正方形AB′C′D′. (1)、如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α;(2)、如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α=30°时.
(1)、如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α;(2)、如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α=30°时.①求∠DAQ的度数;
②若AB=6,求PQ的长度.
25. 如图,抛物线y=ax2+bx(a>0)过点E(8,0),矩形ABCD的边AB在线段OE上(点A在点B的左侧),点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA:AD=1:3. (1)、求抛物线的解析式;(2)、F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值;(3)、在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为 ?若存在,求出点P的坐标;若不存在,请说明理由;(4)、矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL平分矩形的面积时,求抛物线平移的距离.
(1)、求抛物线的解析式;(2)、F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值;(3)、在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为 ?若存在,求出点P的坐标;若不存在,请说明理由;(4)、矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL平分矩形的面积时,求抛物线平移的距离.