江苏省镇江市2020年数学中考模拟试卷(3月)
试卷更新日期:2020-05-20 类型:中考模拟
一、填空题
-
1. 的绝对值是.2. 的立方根是 .3. 计算:(﹣2x﹣3y)(2x﹣3y)= .4. 要使分式 有意义,则字母x的取值范围是 .5. △ABC中,三条中位线围成的三角形周长是15cm,则△ABC的周长是cm.6. 如图△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠C的度数为°.
 7. 两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的众数为 .8. 当 时,一元二次方程 ( 为常数)有两个相等的实数根.9. 若一个圆锥的母线长是3,底面半径是1,则它的侧面展开图的面积是 .10. 如图,将△ABC绕顶点A顺时针旋转60°后得到△AB1C1 , 且C1为BC的中点,AB与B1C1相交于D,若AC=2,则线段B1D的长度为 .
7. 两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的众数为 .8. 当 时,一元二次方程 ( 为常数)有两个相等的实数根.9. 若一个圆锥的母线长是3,底面半径是1,则它的侧面展开图的面积是 .10. 如图,将△ABC绕顶点A顺时针旋转60°后得到△AB1C1 , 且C1为BC的中点,AB与B1C1相交于D,若AC=2,则线段B1D的长度为 . 11. 小红从家到图书馆查阅资料然后返回,她离家的距离y与离家的时间x之间的对应关系如图所示,如果小红离家50分钟时离家的距离为0.3km,那么她在图书馆查阅资料的时间为 .
11. 小红从家到图书馆查阅资料然后返回,她离家的距离y与离家的时间x之间的对应关系如图所示,如果小红离家50分钟时离家的距离为0.3km,那么她在图书馆查阅资料的时间为 . 12. 如图,在 中, ,将直角三角板的直角顶点与 边的中点 重合,直角三角板绕着点 旋转,两条直角边分别交 边于 ,则 的最小值是.
12. 如图,在 中, ,将直角三角板的直角顶点与 边的中点 重合,直角三角板绕着点 旋转,两条直角边分别交 边于 ,则 的最小值是.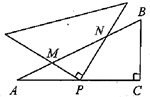
二、单选题
-
13. 下列计算正确的是( )A、3a+2b=5ab B、3a﹣2a=1 C、a6÷a2=a3 D、(﹣a3b)2=a6b214. 下列立体图形中,俯视图是三角形的是( )A、
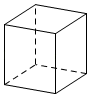 B、
B、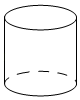 C、
C、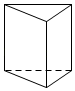 D、
D、 15. 已知 ,则ab的值为( )A、4 B、﹣4 C、﹣8 D、816. 已知方程x2﹣6x+q=0配方后是(x﹣p)2=7,那么方程x2+6x+q=0配方后是( )A、(x﹣p)2=5 B、(x+p)2=5 C、(x﹣p)2=9 D、(x+p)2=717. 如图,已知P是半径为3的⊙A上一点,延长AP到点C,使AC=4,以AC为对角线作▱ABCD,AB=4 ,⊙A交边AD于点E,当▱ABCD面积为最大值时, 的长为( )
15. 已知 ,则ab的值为( )A、4 B、﹣4 C、﹣8 D、816. 已知方程x2﹣6x+q=0配方后是(x﹣p)2=7,那么方程x2+6x+q=0配方后是( )A、(x﹣p)2=5 B、(x+p)2=5 C、(x﹣p)2=9 D、(x+p)2=717. 如图,已知P是半径为3的⊙A上一点,延长AP到点C,使AC=4,以AC为对角线作▱ABCD,AB=4 ,⊙A交边AD于点E,当▱ABCD面积为最大值时, 的长为( )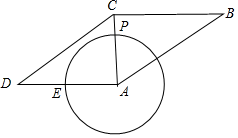 A、 π B、π C、 π D、3π18. 如图,在平面直角坐标系中,点A在一次函数y= x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2 ,AD=1,则OD的最大值是( )
A、 π B、π C、 π D、3π18. 如图,在平面直角坐标系中,点A在一次函数y= x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2 ,AD=1,则OD的最大值是( )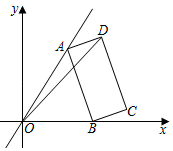 A、 B、 +2 C、 +2 D、
A、 B、 +2 C、 +2 D、三、解答题
-
19. 计算:(1)、 ;(2)、 .20.(1)、解方程: ;(2)、解不等式 ,并把解集表示在数轴上.21. 已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
 22. 为了进一步了解某校九年级1000名学生的身体素质情况,体育老师对该校九年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
22. 为了进一步了解某校九年级1000名学生的身体素质情况,体育老师对该校九年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:组别
次数x
频数(人数)
第1组
80≤x<100
6
第2组
100≤x<120
8
第3组
120≤x<140
12
第4组
140≤x<160
a
第5组
160≤x<180
6

请结合图表完成下列问题:
(1)、求表中a的值;(2)、请把频数分布直方图补充完整;(3)、若在一分钟内跳绳次数少于120次的为测试不合格,试估计该年级学生不合格的人数大约有多少人?23. 现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.(1)、写出甲所拿的垃圾恰好是“厨余垃圾”的概率;(2)、求乙所拿的两袋垃圾不同类的概率.24. 如图,直线l1与l2相交于点P,点P横坐标为﹣1,l1的解析式为y= x+3,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称. (1)、求点B的坐标;(2)、求直线l2的解析式;(3)、若点M为直线l2上一动点,直接写出使△MAB的面积是△PAB的面积的 的点M的坐标;(4)、当x为何值时,l1 , l2表示的两个函数的函数值都大于0?25. 某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即 m/s),交通管理部门在离该公路100m处设置了一速度检测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在点A的北偏东45°方向上.
(1)、求点B的坐标;(2)、求直线l2的解析式;(3)、若点M为直线l2上一动点,直接写出使△MAB的面积是△PAB的面积的 的点M的坐标;(4)、当x为何值时,l1 , l2表示的两个函数的函数值都大于0?25. 某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即 m/s),交通管理部门在离该公路100m处设置了一速度检测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在点A的北偏东45°方向上. (1)、在图中直接标出表示60°和45°的角;(2)、写出点B、点C坐标;(3)、一辆汽车从点B匀速行驶到点C所用时间为15s.请你通过计算,判断该汽车在这段限速路上是否超速?(本小问中 取1.7)26. 如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)、在图中直接标出表示60°和45°的角;(2)、写出点B、点C坐标;(3)、一辆汽车从点B匀速行驶到点C所用时间为15s.请你通过计算,判断该汽车在这段限速路上是否超速?(本小问中 取1.7)26. 如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.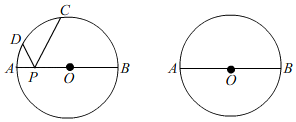 (1)、若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;(2)、若 的长为 π,求“回旋角”∠CPD的度数;(3)、若直径AB的“回旋角”为120°,且△PCD的周长为24+13 ,直接写出AP的长.27. 如图,在平面直角坐标系中,一次函数 的图像分别交x、y轴于点A、B,抛物线 经过点A、B,点P为第四象限内抛物线上的一个动点.
(1)、若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;(2)、若 的长为 π,求“回旋角”∠CPD的度数;(3)、若直径AB的“回旋角”为120°,且△PCD的周长为24+13 ,直接写出AP的长.27. 如图,在平面直角坐标系中,一次函数 的图像分别交x、y轴于点A、B,抛物线 经过点A、B,点P为第四象限内抛物线上的一个动点. (1)、求此抛物线对应的函数表达式;(2)、如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;(3)、如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.28. 如图,在平面直角坐标系中,直线 分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE.动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
(1)、求此抛物线对应的函数表达式;(2)、如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;(3)、如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.28. 如图,在平面直角坐标系中,直线 分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE.动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点. (1)、求点B的坐标和OE的长;(2)、设点Q2为(m , n),当 tan∠EOF时,求点Q2的坐标;(3)、根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.①延长AD交直线BC于点Q3 , 当点Q在线段Q2Q3上时,设Q3Q=s , AP=t , 求s关于t的函数表达式.②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.
(1)、求点B的坐标和OE的长;(2)、设点Q2为(m , n),当 tan∠EOF时,求点Q2的坐标;(3)、根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.①延长AD交直线BC于点Q3 , 当点Q在线段Q2Q3上时,设Q3Q=s , AP=t , 求s关于t的函数表达式.②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.