黑龙江哈尔滨市松北区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期：2020-05-20 类型：期末考试
一、单选题
-
1. 若线段a，b，c组成直角三角形，则它们的比可以为（ ）A、2∶3∶4 B、7∶24∶25 C、5∶12∶14 D、4∶6∶102. 下列方程，是一元二次方程的是（ ）
① ，② ，③ ， ④
A、①② B、①②④ C、①③④ D、②④3. 下列图形中，不是轴对称图形的是（ ）A、矩形 B、菱形 C、平行四边形 D、正方形4. 一次函数 在平面直角坐标系内的图像如图所示，则k和b的取值范围是（ ）
A、 ， B、 ， C、 ， D、 ，5. 下列命题的逆命题正确的是（ ）A、如果两个角都是45°，那么它们相等 B、全等三角形的周长相等 C、同位角相等，两直线平行 D、若a=b，则6. 在▱ABCD中，∠A：∠B=7：2，则∠C等于（ ）A、40° B、80° C、120° D、140°7. 某机械厂七月份生产零件50万个，第三季度生产零件196万个．设该厂八、九月份平均每月的增长率为x，那么x满足的方程是（ ）A、50（1+x2）=196 B、50+50（1+x2）=196 C、50+50（1+x）+50（1+x2）=196 D、50+50（1+x）+50（1+2x）=1968. 将直线 平移后，得到直线 ，则原直线（ ）A、沿y轴向上平移了8个单位 B、沿y轴向下平移了8个单位 C、沿x轴向左平移了8个单位 D、沿x轴向右平移了8个单位9. 顺次连结菱形各边中点所得到四边形一定是（ ）A、平行四边形 B、正方形 C、矩形 D、菱形10. 梅凯种子公司以一定价格销售“黄金1号”玉米种子，如果一次购买10千克以上(不含10千克)的种子，超过10千克的那部分种子的价格将打折，并依此得到付款金额y(单位：元)与一次购买种子数量x（单位：千克)之间的函数关系如图所示．下列四种说法：①一次购买种子数量不超过10千克时，销售价格为5元/千克；
②一次购买30千克种子时，付款金额为100元；
③一次购买10千克以上种子时，超过10千克的那部分种子的价格打五折：
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱．
其中正确的个数是
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 关于 的一元二次方程 有一个解是 ，则 ．12. 若一个三角形的三边长分别为5、12、13，则此三角形的面积为 ．13. 如图，在平行四边形ABCD中，∠BAD的平分线AE交边CD于E，▱ABCD的周长是16cm，EC=2cm，则BC=.
14. 如果关于x的方程 没有实数根，则k的取值范围为.15. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，∠ACD=3∠BCD，E是斜边AB的中点，则∠ECD的度数为度.
16. 如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为 ．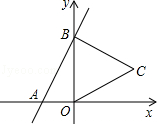
17. 已知：等腰三角形ABC的面积为30 ，AB=AC= 10 ，则底边BC的长度为 m.18. 如图，在矩形ABCD中，AD=10，AB=8，点P在AD上，且BP=BC，点M在线段BP上，点N在线段BC的延长线上，且MP=NC，连接MN交线段PC于点F，过点M作ME⊥PC于点E，则EF= .
三、综合题
-
19. 解方程：(1)、(2)、20. 如图所示的方格纸中的每个小正方形的边长均为1，点A、B在小正方形的顶点上.在图中画出△ABC(点C在小正方形的顶点上)，使△ABC为直角三角形.
21. 如图所示，已知一次函数的图象直线AB经过点(0，6)和点(-2，0).
(1)、求这个函数的解析式；(2)、直线AB与x轴交于点A，与y轴交于点B，求△AOB的面积.22. 如图，DE是平行四边形ABCD中的∠ADC的平分线，EF∥AD，交DC于F.
(1)、求证：四边形AEFD是菱形；(2)、如果∠A=60度，AD=5，求菱形AEFD的面积.23. 哈市某专卖店销售某品牌服装，设服装进价为80元，当每件服装售价为240元时，月销售为200件，该专卖店为提高经营利润，准备采取降价的方式进行促销，经市场调查发现：当每件价格每下降10元时，月销售量就会增加20件，设每件服装售价为x(元)，该专卖店的月利润为y(元).(1)、求出y与x的函数关系式(不要求写出x的取值范围)；(2)、该专卖店要获得最大月利润，售价应定为每件多少元？最大利润是多少？
