黑龙江双鸭山市2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-05-20 类型：期末考试

进入出卷网下载

一、填空题

1. ${(- 3)}^{0} + \sqrt{12} \times \sqrt{3}$ ＝．

查看试题解析
2. 函数y= –1的自变量x的取值范围是．

查看试题解析
3. 如图，平行四边形ABCD的对角线AC，BD相交于点O，请你添加一个适当的条件使其成为菱形（只填一个即可）．

查看试题解析
4. 如图，在平面直角坐标系xOy中，点A（0，2），B（4，0），点N为线段AB的中点，则点N的坐标为．

查看试题解析
5. 实数a、b在数轴上的位置如图所示，化简 $| a - b | - \sqrt{a^{2}}$ = ．

查看试题解析
6. 我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形．现有一个对角线分别为6cm和8cm的菱形，它的中点四边形的对角线长是．

查看试题解析
7. 由作图可知直线 $y = - 5 x + 2$ 与 $y = - 5 x - 3$ 互相平行，则方程组 ${\begin{array}{l} y = - 5 x + 2 \\ y = - 5 x - 3 \end{array}$ 的解的情况为.

查看试题解析
8. 一组正整数2，4，5， $x$ 从小到大排列，已知这组数据的中位数和平均数相等，那么 $x$ 的值是.

查看试题解析
9. 正方形ABCD的边长是4，点P是AD边的中点，点E是正方形边上的一点．若△PBE是等腰三角形，则腰长为 .

查看试题解析
10. 正方形 $A_{1} B_{1} C_{1} O$ 、 $A_{2} B_{2} C_{2} C_{1}$ 、 $A_{3} B_{3} C_{3} C_{2}$ 、…按如图所示的方式放置.点 $A_{1}$ 、 $A_{2}$ 、 $A_{3}$ 、…和点 $C_{1}$ 、 $C_{2}$ 、 $C_{3}$ 、…分别在直线 $y = x + 1$ 和 $x$ 轴上，则点 $B_{n}$ 的坐标是．（ $n$ 为正整数）

查看试题解析
11. 如图，在平面直角坐标系xOy中，直线 $l_{1}$ ， $l_{2}$ 分别是函数 $y = k_{1} x + b_{1}$ 和 $y = k_{2} x + b_{2}$ 的图象，则可以估计关于x的不等式 $k_{1} x + b_{1} > k_{2} x + b_{2}$ 的解集为．

查看试题解析

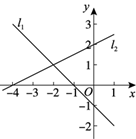
二、选择题

12. 下列各式中，化简后能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{12}$ B、 $\sqrt{8}$ C、 $\sqrt{\frac{2}{3}}$ D、 $\sqrt{0.2}$

查看试题解析
13. 以下列各组数为边长，不能构成直角三角形的是（）

A、5，12，13 B、1，2， $\sqrt{5}$ C、1， $\sqrt{3}$ ，2 D、4，5，6

查看试题解析
14. 下列函数的图象不经过第一象限，且y随x的增大而减小的是（）

A、 $y = - x$ B、 $y = x + 1$ C、 $y = - 2 x + 1$ D、 $y = x - 1$

查看试题解析
15. 下表是两名运动员10次比赛的成绩， $s_{1}^{2}$ ， $s_{2}^{2}$ 分别表示甲、乙两名运动员测试成绩的方差，则有（）

8分

9分

10分

甲（频数）

4

2

4

乙（频数）

3

4

3

A、 $s_{1}^{2} > s_{2}^{2}$ B、 $s_{1}^{2} = s_{2}^{2}$ C、 $s_{1}^{2} < s_{2}^{2}$ D、无法确定

查看试题解析
16. 小亮从家步行到公交车站台，等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法不正确的是（）

A、他离家8km共用了30min B、他等公交车时间为6min C、他步行的速度是100m/min D、公交车的速度是350m/min

查看试题解析
17. 对于任意不相等的两个实数 $a$ ， $b$ ，定义运算如下： $a ※ b = \frac{\sqrt{a + b}}{a - b}$ .如果 $3 ※ 2 = \frac{\sqrt{3 + 2}}{3 - 2} = \sqrt{5}$ ，那么 $8 ※ 12$ 的值为（）

A、 $\frac{\sqrt{5}}{2}$ B、 $- \frac{\sqrt{5}}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $- \frac{\sqrt{2}}{2}$

查看试题解析
18. 如图，点 $A$ ， $B$ ， $E$ 在同一条直线上，正方形 $A B C D$ ，正方形 $B E F G$ 的边长分别为3，4， $H$ 为线段 $D F$ 的中点，则 $B H$ 的长为（）

A、 $3 \sqrt{2}$ B、 $4 \sqrt{2}$ C、 $3 \sqrt{2}$ 或 $4 \sqrt{2}$ D、 $\frac{5 \sqrt{2}}{2}$

查看试题解析
19. 为了丰富学生课外小组活动，培养学生动手操作能力，王老师让学生把5m长的彩绳截成2m或1m的彩绳，用来做手工编织，在不造成浪费的前提下，你有几种不同的截法（）

A、4 B、3 C、2 D、1

查看试题解析
20. 如图所示，在正方形 $A B C D$ 中，边长为2的等边三角形 $A E F$ 的顶点 $E$ ， $F$ 分别在 $B C$ 和 $C D$ 上.下列结论：① $C E = C F$ ；② $∠ A E B = 75 °$ ；③ $B E + D F = E F$ ；④ $S_{正方形 A B C D} = 2 + \sqrt{3}$ .其中结论正确的序号是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

三、综合题

21. 计算：

(1)、 $\sqrt{14} \div \sqrt{6} \times \sqrt{\frac{27}{2}}$ ；

(2)、 $(\sqrt{2} - 2 \sqrt{3}) (\sqrt{2} + 2 \sqrt{3})$ .

查看试题解析
22. 在平面直角坐标系xOy中，已知一次函数 $y = - \frac{1}{2} x + 1$ 的图象与x轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ．

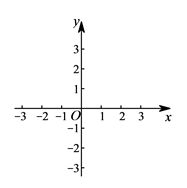(1)、求 $A$ ， $B$ 两点的坐标；

(2)、在给定的坐标系中画出该函数的图象；

(3)、点M（ $-$ 1，y₁），N（3，y₂）在该函数的图象上，比较y₁与y₂的大小.

查看试题解析
23. 如图，在四边形 $A B C D$ 中， $∠ A B C = 90 °$ ， $C D ⊥ A D$ 于点 $D$ ， $A D^{2} + C D^{2} = 2 A B^{2}$ .求证 $A B = B C$ .

查看试题解析
24. 甲、乙两校的学生人数基本相同，为了解这两所学校学生的数学学业水平，在同一次测试中，从两校各随机抽取了30名学生的测试成绩进行调查分析，其中甲校已经绘制好了条形统计图，乙校只完成了一部分．
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87

89 79 54 88 92 90 87 68 76 94 84 76 69 83 92

乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92

73 76 92 84 57 87 89 88 94 83 85 80 94 72 90

(1)、请根据乙校的数据补全条形统计图；

(2)、两组样本数据的平均数、中位数、众数如下表所示，请补全表格；

平均数

中位数

众数

甲校

83.4

87

89

乙校

83.2

(3)、两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些，
请为他们各写出一条可以使用的理由；

甲校：．乙校：．

(4)、综合来看，可以推断出校学生的数学学业水平更好一些，理由为．

查看试题解析
25. 一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量保持不变，容器内水量 $y$ （单位： $L$ ）与时间 $x$ （单位： $\min$ ）的部分函数图象如图所示，请结合图象信息解答下列问题：

(1)、求出水管的出水速度；

(2)、求 $8 \min$ 时容器内的水量；

(3)、从关闭进水管起多少分钟时，该容器内的水恰好放完？

查看试题解析
26. 如图，四边形 $A B C D$ 是正方形， $E$ 是 $B C$ 边所在直线上的点， $∠ A E F = 90 °$ ，且 $E F$ 交正方形外角 $∠ D C G$ 的平分线 $C F$ 于点 $F$ .

⑴当点 $E$ 在线段 $B C$ 中点时（如图①），易证 $A E = E F$ ，不需证明；

⑵当点 $E$ 在线段 $B C$ 上（如图②）或在线段 $B C$ 延长线上（如图③）时，（1）中的结论是否仍然成立？请写出你的猜想，并选择图②或图③的一种结论给予证明.

查看试题解析
27. 某产品生产车间有工人10名．已知每名工人每天可生产甲种产品12个或乙种产品10个，且每生产一个甲种产品可获得利润100元，每生产一个乙种产品可获得利润180元．在这10名工人中，车间每天安排x名工人生产甲种产品，其余工人生产乙种产品．

(1)、请写出此车间每天获取利润y（元）与x（人）之间的函数关系式；

(2)、若要使此车间每天获取利润为14400元，要派多少名工人去生产甲种产品？

(3)、若要使此车间每天获取利润不低于15600元，你认为至少要派多少名工人去生产乙种产品才合适？

查看试题解析
28. 如图，在平面直角坐标系xOy中，直线 $l$ 的表达式为 $y = 2 x - 6$ ，点A ， B的坐标分别为（1，0），（0，2），直线AB与直线 $l$ 相交于点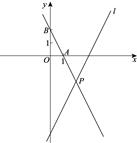P ．

(1)、求直线AB的表达式；

(2)、求点P的坐标；

(3)、若直线 $l$ 上存在一点C ，使得△APC的面积是△APO的面积的2倍，直接写出点C的坐标．

查看试题解析

	8分	9分	10分
甲（频数）	4	2	4
乙（频数）	3	4	3

	平均数	中位数	众数
甲校	83.4	87	89
乙校	83.2