江苏省连云港市2020年数学中考模拟试卷（二）

试卷更新日期：2020-05-20 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{2}{3}$ 的倒数是（　　）

A、1 B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、2

查看试题解析
2. 下列几何体中，从正面看得到的平面图形是圆的是（　　）

A、 B、 C、 D、

查看试题解析
3. 某地区连续10天的最高气温统计如下表，则该地区这10天最高气温的众数是（）

最高气温(℃)

18

19

20

21

22

天数

1

2

2

3

2

A、20 B、20.5 C、21 D、22

查看试题解析
4. 某单位进行内部抽奖，共准备了100张抽奖券，设一等奖10个，二等奖20个，三等奖30个。若每张抽奖券获奖的可能性相同，则1张抽奖券中奖的概率是（）

A、0.1 B、0.2 C、0.3 D、0.6

查看试题解析
5. 在下列四个图案中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 下列计算中，错误的是（　　）

A、5a³﹣a³＝4a³ B、（﹣a）²•a³＝a⁵ C、（a﹣b）³•（b﹣a）²＝（a﹣b）⁵ D、2^m•3ⁿ＝6^m+n

查看试题解析
7. 2cos 30°的值等于(　　)

A、 1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
8. 如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M.则下列结论：①∠AME＝90°，②∠BAF＝∠EDB，③AM＝ $\frac{2}{3}$ MF，④ME+MF＝ $\sqrt{2}$ MB．其中正确结论的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

9. 函数 $y = \frac{\sqrt{x}}{x - 2}$ 中，自变量 $x$ 的取值范围是．

查看试题解析
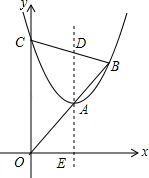
10. 已知一组数据x₁+x₂+…+x_n＝36，平均数 $\bar{x}$ ＝1.8，则n＝．

查看试题解析
11. 如图，抛物线y＝x²+bx+c（c＞0）与y轴交于点C，顶点为A，抛物线的对称轴交x轴于点E，交BC于点D，tan∠AOE＝ $\frac{3}{2}$ ．直线OA与抛物线的另一个交点为B．当OC＝2AD时，c的值是．

查看试题解析
12. 若 $\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{1}{2}$ ，则 $\frac{a + c + e}{b + d + f}$ = ．

查看试题解析
13. 如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器零刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒4度的速度旋转，CP与量角器的半圆弧交于点E，第18秒时，点E在量角器上对应的读数是度．

查看试题解析
14. 如图，在平行四边形ABCD中，∠B＝120°，AB与CD之间的距离是 $4 \sqrt{3}$ ，AB＝28，在AB上取一点E（AE＜BE），使得∠DEC＝120°，则AE＝．

查看试题解析
15. 如图，E，F分别是矩形ABCD边AD、BC上的点，且△ABG，△DCH的面积分别为12和18，则图中阴影部分的面积为．

查看试题解析
16. 如图，在△ABC中，∠C＝90°，AB＝10， $\tan A = \frac{3}{4}$ ，经过点C且与边AB相切的动圆与CA、CB分别交于点D、E，则线段DE长度的最小值是．

查看试题解析

三、解答题

17. 计算：

(1)、 $2 \sin 30^{°} - \tan 45^{°}$

(2)、 ${(3.14 - π)}^{0} + \sqrt{8} - 4 \sin 45^{°} + {(\frac{1}{3})}^{- 1}$

查看试题解析
18. 先化简，再求值： $(2 - \frac{x - 1}{x + 1}) \div (\frac{x^{2} + 6 x + 9}{x^{2} - 1})$ ，其中 $x = 2$ ．

查看试题解析
19. 解不等式组 ${\begin{array}{l} \frac{3 x + 14}{4} > 2 x - 9 \\ 4 x + 6 \geq 3 x + 7 \end{array}$

查看试题解析
20. 已知关于x的一元二次方程x²+（2k+1）x+k²＝0有实数根．

(1)、求k的取值范围．

(2)、设方程的两个实数根分别为x₁、x₂ ，若2x₁x₂﹣x₁﹣x₂＝1，求k的值．

查看试题解析
21. 如图，点E是矩形ABCD中CD边上一点， $△ B C E$ 沿BE折叠为 $△ B F E$ ，点F落在AD上

(1)、求证： $△ A B F ∽ △ D F E$ ；

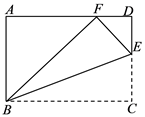(2)、若 $\sin ∠ D F E = \frac{2}{3}$ ，求 $\tan ∠ E B C$ 的值．

查看试题解析
22. 为了传承中华民族优秀传统文化，我市某中学举行“汉字听写”比赛，赛后整理参赛学生的成绩，将学生的成绩分为A ， B ， C ， D四个等级，并将结果绘制成图1的条形统计图和图2扇形统计图，但均不完整．请你根据统计图解答下列问题：

(1)、求参加比赛的学生共有多少名？并补全图1的条形统计图．

(2)、在图2扇形统计图中，m的值为，表示“D等级”的扇形的圆心角为度；

(3)、组委会决定从本次比赛获得A等级的学生中，选出2名去参加全市中学生“汉字听写”大赛．已知A等级学生中男生有1名，请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率．

查看试题解析
23. 矩形ABCD的对角线相交于点O．DE∥AC，CE∥BD．

(1)、求证：四边形OCED是菱形；

(2)、若∠ACB＝30°，菱形OCED的面积为 $8 \sqrt{3}$ ，求AC的长．

查看试题解析
24. 如图，一农户要建一个矩形猪舍，猪舍的一边利用长为15m的住房墙，另外三边用27m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长，宽分别为多少米时，猪舍面积为96m²？

查看试题解析
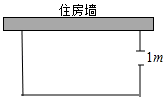25. 州政府投资3个亿拟建的恩施民族高中，它位于北纬31°，教学楼窗户朝南，窗户高度为h米，此地一年的冬至这一天的正午时刻太阳光与地面的夹角最小为α，夏至这一天的正午时刻太阳光与地面的夹角最大为β．若你是一名设计师，请你为教学楼的窗户设计一个直角形遮阳蓬BCD，要求它既能最大限度地遮挡夏天炎热的阳光，又能最大限度地使冬天温暖的阳光射入室内（如图）．根据测量测得∠α=32.6°，∠β=82.5°，h=2.2米．请你求出直角形遮阳蓬BCD中BC与CD的长各是多少？（结果精确到0.1米）
（参考数据：sin32.6°=0.54，sin82.5°=0.99，tan32.6°=0.64，tan82.5°=7.60）

查看试题解析
26. 如图，抛物线y＝ax²+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于A（﹣2，0），点B（4，0）．

(1)、求抛物线的解析式；

(2)、若点M是抛物线上的一动点，且在直线BC的上方，当S_△MBC取得最大值时，求点M的坐标；

(3)、在直线的上方，抛物线是否存在点M，使四边形ABMC的面积为15？若存在，求出点M的坐标；若不存在，请说明理由．

查看试题解析
27. 如图，已知四边形ABCD中，AB⊥AD，BC∥AD，E为AB的中点，且EC、ED分别为∠BCD、∠ADC的角平分线，EF⊥CD交BC的延长线于点G，连接DG.

(1)、求证：CE⊥DE；

(2)、若AB=6，求CF·DF的值；

(3)、当△BCE与△DFG相似时， $\frac{BC}{A D}$ 的值是.

查看试题解析

最高气温(℃)	18	19	20	21	22
天数	1	2	2	3	2