江苏省淮安市淮安区2020年九年级下学期数学学业质量调研试卷

试卷更新日期：2020-05-20 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列函数解析式中，一定为二次函数的是（）

A、 $y = 3 x - 1$ B、 $y = a x^{2} + b x + c$ C、 $s = 2 t^{2} - 2 t + 1$ D、 $y = x^{2} + \frac{1}{x}$

查看试题解析
2. 已知 $\frac{a}{b}$ = $\frac{2}{3}$ ，那么 $\frac{a}{a + b}$ 的值为（　　）

A、 $\frac{1}{3}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{3}{4}$

查看试题解析
3. 下列各线段中，能成比例的是（）

A、3cm、5cm、7cm、9cm B、2cm、5cm、6cm、8cm C、3cm、6cm、9cm、18cm D、1cm、3cm、4cm、6cm

查看试题解析
4. 三角形三边之比3：5：7，与它相似的三角形最长边是21cm，另两边之和是（　　）

A、15cm B、18cm C、21cm D、24cm

查看试题解析
5. 等腰三角形底边长为10cm，周长为36cm，那么底角的余弦等于（）．

A、 $\frac{5}{13}$ B、 $\frac{12}{13}$ C、 $\frac{10}{13}$ D、 $\frac{5}{12}$

查看试题解析
6. 分别写有数字0，﹣1，﹣2，1，3的五张卡片，除数字不同外其他均相同，从中任抽一张，那么抽到负数的概率是（　　）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
7. 如图，在Rt△ABC中，∠C＝90°，sinA＝ $\frac{4}{5}$ ，AC＝6cm，则BC的长度为(　　)

A、6cm B、7cm C、8cm D、9cm

查看试题解析
8.
如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（　　）

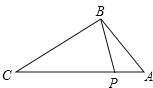A、∠ABP=∠C B、∠APB=∠ABC C、 $\frac{A P}{A B} = \frac{A B}{A C}$ D、 $\frac{A B}{B P} = \frac{A C}{C B}$

查看试题解析

二、填空题

9. 若两个相似多边形的相似比是2：3，则它们的面积比等于．

查看试题解析
10. 直线y=-2与抛物线y=-x²的交点有个．

查看试题解析
11. 在△ABC中，∠C＝90°，sinA＝ $\frac{4}{5}$ ，则tanB＝．

查看试题解析
12. 顺次连接三角形三边的中点，所得的三角形与原三角形的相似比是．

查看试题解析
13. 把抛物线y=x²向下平移4个单位，所得的抛物线的函数关系式为．

查看试题解析
14. △ABC中，已知 ${(\sqrt{2} \sin A - 1)}^{2} + | \tan B - \frac{\sqrt{3}}{3} | = 0$ ，∠A、∠B为锐角，则∠C=°

查看试题解析
15. 已知点 $C$ 是线段 $A B$ 的黄金分割点，且 $A C > C B$ ，若 $A B = 2$ ，则 $A C$ 长为.

查看试题解析
16. 若关于x的函数 $y = {kx}^{2} + 2 x - 1$ 与x轴仅有一个公共点，则实数k的值为.

查看试题解析

三、解答题

17. 计算：

(1)、 $2 \sin 30^{°} - \tan 45^{°}$

(2)、 ${(3.14 - π)}^{0} + \sqrt{8} - 4 \sin 45^{°} + {(\frac{1}{3})}^{- 1}$

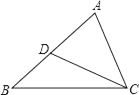
查看试题解析
18. 如图，点D在△ABC的边AB上，∠ACD=∠B，AD=8cm，DB=10cm，求AC的长．

查看试题解析
19. 在一张比例尺为 $1 : 20$ 的地图上，有一块多边形区域的周长是 $24 cm$ ，面积是 $20 {cm}^{2}$ ，求这个区域的实际周长和面积．

查看试题解析
20. 求满足下列条件的锐角x：

(1)、 $\cos x = \frac{\sqrt{3}}{2}$

(2)、 $\sqrt{3} \tan x - 3 = 0$

查看试题解析
21. 已知抛物线 $y = a x^{2}$ 的图象经过点A（2，-8），求：

(1)、该抛物线的解析式；

(2)、判断点B（3，-18）是否在该抛物线上；

(3)、求出此抛物线上纵坐标是-50的点的坐标．

查看试题解析
22. 在△ABC中，tanA＝ $\frac{\sqrt{3}}{3}$ ，tanB＝1，CD⊥AB于点D，且BD＝4，请画出示意图并且求边AB的长．

查看试题解析
23. 如图，某公路隧道横截面为抛物线，其最大高度为6米，底部宽度OM为12米．现以O点为原点，OM所在直线为x轴建立直角坐标系．

(1)、写出点M及抛物线顶点P的坐标；

(2)、求这条抛物线的解析式．

查看试题解析
24. 如图，在△ABC中，AB＝AC，点D、E分别在BC、AB上，且∠BDE＝∠CAD．

(1)、求证：△BDE∽△CAD；

(2)、求证：△ADE∽△ABD．

查看试题解析
25. 如图，在某建筑物AC上，挂着“魅力湖州”的宣传条幅BC，小明站在点F处，看条幅顶端B，测得仰角为30°，再往条幅方向前行20米到达点E处，看到条幅顶端B，测得仰角为60°，求宣传条幅BC的长（小明的身高不计）．

查看试题解析
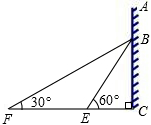26. 如图，花丛中有一路灯 $A B$ .在灯光下，小明在点D处的影长 $D E = 3 m$ ，沿 $B D$ 方向行走到达点G， $D G = 5 m$ ，这时小明的影长 $G H = 5 m$ .如果小明的身高为1.7m，求路灯 $A B$ 的高度.（精确到0.1m)

查看试题解析
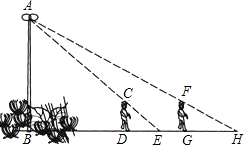27. 如图，在Rt△ABC中，∠C=90°，AC=20cm，BC=15cm，现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿CB向点B方向运动，如果点P的速度是4cm/秒，点Q的速度是2cm/秒，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动时间为t秒．求：

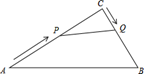(1)、当t=3秒时，这时，P，Q两点之间的距离是多少？

(2)、若△CPQ的面积为S，求S关于t的函数关系式．

(3)、当t为多少秒时，以点C，P，Q为顶点的三角形与△ABC相似？

查看试题解析