江苏省连云港市灌南县2020年数学中考一模试卷
试卷更新日期:2020-05-20 类型:中考模拟
一、单选题
-
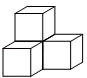
1. 的倒数是( )A、 B、 C、 D、2. 四个大小相同的正方体搭成的几何体如图所示,其左视图是( ).
 A、
A、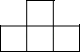 B、
B、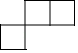 C、
C、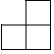 D、
D、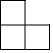 3. 数据4,3,2,1,3的众数是( )A、4 B、3 C、2 D、14. 一个布袋里装有10个只有颜色不同的球,其中4个黄球,6个白球.从布袋里任意摸出1个球,则摸出的球是黄球的概率为( )A、 B、 C、 D、5. 下列图形中,不是中心对称图形的是( )A、平行四边形 B、矩形 C、菱形 D、等边三角形6. 下列运算正确的是( )A、 B、 C、 D、7. 在△ABC中,∠A,∠B都是锐角,且sinA= , cosB= ,则△ABC是( )A、直角三角形 B、钝角三角形 C、锐角三角形 D、不能确定8. 如图,正方形ABCD中,E,F分别为BC,CD的中点,AF与DE交与点G.则下列结论中:①AF⊥DE;②AD=BG;③GE+GF= GC;④S△AGB=2S四边形ECFG.其中正确的是( )
3. 数据4,3,2,1,3的众数是( )A、4 B、3 C、2 D、14. 一个布袋里装有10个只有颜色不同的球,其中4个黄球,6个白球.从布袋里任意摸出1个球,则摸出的球是黄球的概率为( )A、 B、 C、 D、5. 下列图形中,不是中心对称图形的是( )A、平行四边形 B、矩形 C、菱形 D、等边三角形6. 下列运算正确的是( )A、 B、 C、 D、7. 在△ABC中,∠A,∠B都是锐角,且sinA= , cosB= ,则△ABC是( )A、直角三角形 B、钝角三角形 C、锐角三角形 D、不能确定8. 如图,正方形ABCD中,E,F分别为BC,CD的中点,AF与DE交与点G.则下列结论中:①AF⊥DE;②AD=BG;③GE+GF= GC;④S△AGB=2S四边形ECFG.其中正确的是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 函数y= 中自变量x的取值范围是 .
10. 一组数据 , , , , 的平均数为 ,则 为.11. 二次函数 的图像的顶点坐标是.12. 已知 ,则 =.13. 如图,AB是⊙O的直径,CD是⊙O的弦,∠BAD=60°,则∠ACD=°. 14. 如图,在 中,点 在 上, 与 相交于点 ,若 ,则 .
14. 如图,在 中,点 在 上, 与 相交于点 ,若 ,则 . 15. 如图,点 是矩形 的对角线 上一点,过点 作 交 于 ,交 于 ,若 , ,则图中阴影部分的面积为.
15. 如图,点 是矩形 的对角线 上一点,过点 作 交 于 ,交 于 ,若 , ,则图中阴影部分的面积为.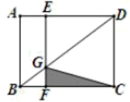 16. 如图,在 中, , , ,经过点 且与边 相切的动圆与 , 分别相交于点 , ,则线段 长度的最小值是.
16. 如图,在 中, , , ,经过点 且与边 相切的动圆与 , 分别相交于点 , ,则线段 长度的最小值是.
三、解答题
-
17. 计算:18. 先化简,再求值: ,其中 .19. 解不等式组:20. 已知关于 的方程 .(1)、求证:不论 取何实数,该方程都有两个不相等的实数根;(2)、若该方程的一个根为 ,求该方程的另一个根.21. 折叠矩形ABCD,使点D落在BC边上的点F处.
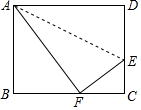 (1)、求证:△ABF∽△FCE;(2)、若DC=8,CF=4,求矩形ABCD的面积S.22. “食品安全”受到全社会的广泛关注,育才中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)、求证:△ABF∽△FCE;(2)、若DC=8,CF=4,求矩形ABCD的面积S.22. “食品安全”受到全社会的广泛关注,育才中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: (1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;(2)、请补全条形统计图;(3)、若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为 ,现从中随机抽取 人参加食品安全知识竞赛,则恰好抽到 个男生和 个女生的概率.23. 如图,矩形ABCD对角线相交于O点,DE∥AC,CE∥BD,连接BE.
(1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;(2)、请补全条形统计图;(3)、若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为 ,现从中随机抽取 人参加食品安全知识竞赛,则恰好抽到 个男生和 个女生的概率.23. 如图,矩形ABCD对角线相交于O点,DE∥AC,CE∥BD,连接BE. (1)、求证:四边形OCED是菱形;(2)、若∠AOD=120°,CD=2,求DE和tan∠DBE的值.24. 如图,在 中, , , ,点 从点 开始沿 边向点 以 的速度移动,同时,点 从点 开始沿 边向点 以 的速度移动(到达点 ,移动停止).
(1)、求证:四边形OCED是菱形;(2)、若∠AOD=120°,CD=2,求DE和tan∠DBE的值.24. 如图,在 中, , , ,点 从点 开始沿 边向点 以 的速度移动,同时,点 从点 开始沿 边向点 以 的速度移动(到达点 ,移动停止). (1)、如果 , 分别从 , 同时出发,那么几秒后, 的长度等于 ?(2)、在(1)中, 的面积能否等于 ?请说明理由.25. 如图,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1: .
(1)、如果 , 分别从 , 同时出发,那么几秒后, 的长度等于 ?(2)、在(1)中, 的面积能否等于 ?请说明理由.25. 如图,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1: . (1)、求加固后坝底增加的宽度AF;(2)、求完成这项工程需要土石多少立方米.(结果保留根号)26. 如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .
(1)、求加固后坝底增加的宽度AF;(2)、求完成这项工程需要土石多少立方米.(结果保留根号)26. 如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .
 (1)、直接写出抛物线的解析式和直线 的解析式;(2)、当点 在线段 上运动时,直接写出线段 长度的最大值;(3)、当点 在线段 上运动时,若 是以 为腰的等腰直角三角形时,求 的值;(4)、当以 、 、 、 为顶点的四边形是平行四边形时,求出 的值.27. 如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)、直接写出抛物线的解析式和直线 的解析式;(2)、当点 在线段 上运动时,直接写出线段 长度的最大值;(3)、当点 在线段 上运动时,若 是以 为腰的等腰直角三角形时,求 的值;(4)、当以 、 、 、 为顶点的四边形是平行四边形时,求出 的值.27. 如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.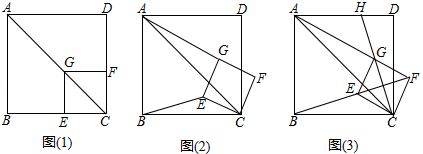 (1)、证明与推断:
(1)、证明与推断:①求证:四边形CEGF是正方形;
②推断: 的值为▲:
(2)、探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)、拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2 ,则BC=.