湖北省武汉市2020年数学中考模拟试卷（三）

试卷更新日期：2020-05-20 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2$ 的相反数是（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列二次根式中，无论x取什么值都有意义的是（　　）

A、 $\sqrt{x^{2} - 5}$ B、 $\sqrt{- x - 5}$ C、 $\sqrt{x}$ D、 $\sqrt{x^{2} + 1}$

查看试题解析
3. 下列事件中，属于必然事件的是（）

A、三角形的外心到三边的距离相等 B、某射击运动员射击一次，命中靶心 C、任意画一个三角形，其内角和是 180° D、抛一枚硬币，落地后正面朝上

查看试题解析
4. 在平面直角坐标系中，已知点 $P (a^{2} + 2, 5)$ ，则点 $P$ 关于直线 $m$ （直线 $m$ 上各点的横坐标都为 $- 2$ ）对称点的坐标是（　　　　）

A、 $(- a^{2} + 6, 5)$ B、 $(- a^{2} - 6, 5)$ C、 $(a^{2} - 6, 5)$ D、 $(- a^{2} + 4, 5)$

查看试题解析
5. 下列立体图形 ①长方体②圆锥③圆柱④球中，左视图可能是长方形的有（　　）

A、① B、①② C、①③ D、①④

查看试题解析
6. 甲，乙两人练习跑步，若乙先跑10米，则甲跑5秒就可以追上乙；若乙先跑2秒，则甲跑4秒就可追上乙.若设甲的速度为x米/秒，乙的速度为y米/秒，则下列方程组中正确的是（　　）

A、 ${\begin{array}{l} 5 x = 5 y + 10 \\ 4 x = 4 y + 2 y \end{array}$ B、 ${\begin{array}{l} 5 x - 5 y = 10 \\ 4 x + 2 y = 4 y \end{array}$ C、 ${\begin{array}{l} 5 x + 10 = 5 y \\ 4 x - 4 y = 2 \end{array}$ D、 ${\begin{array}{l} 5 x - 5 y = 10 \\ 4 x - 2 = 4 y \end{array}$

查看试题解析
7. 若一个袋子中装有形状与大小均完全相同的4张卡片，4张卡片上分别标有数字﹣2，﹣1，2，3，现从中任意抽出其中两张卡片分别记为x，y，并以此确定点P（x，y），那么点P落在直线y=﹣x+1上的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
8. 课间操时，小明、小丽、小亮的位置如图所示，小明对小亮说：如果我的位置用（0，0）表示，小丽的位置用（2，1）表示，那么你的位置可以表示成（）

A、（5，4） B、（4，5） C、（3，4） D、（4，3）

查看试题解析
9. 关于二次函数y＝ $\frac{1}{2}$ (x+1)²的图象，下列说法正确的是（）

A、开口向下 B、经过原点 C、对称轴右侧的部分是下降的 D、顶点坐标是(﹣1，0)

查看试题解析
10. 如图，AB是⊙O的直径，点C为⊙O外一点，CA、CD是⊙O的切线，A、D为切点，连接BD、AD ．若∠ACD＝48°，则∠DBA的大小是（）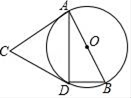

A、32° B、48° C、60° D、66°

查看试题解析

二、填空题

11. 已知 $a < 0, b > 0$ ，化简 $\sqrt{{(a - b)}^{2}} =$

查看试题解析
12. 跳远运动员李阳对训练效果进行测试.6次跳远的成绩如下：7.5，7.7，7.6，7.7，7.9，7.8（单位：m）这六次成绩的平均数为7.7m，方差为 $\frac{1}{60}$ .如果李阳再跳一次，成绩为7.7m.则李阳这7次跳远成绩的方差（填“变大”、“不变”或“变小”）.

查看试题解析
13. 计算： $\frac{6}{a^{2} -9} - \frac{1}{a-3}$ =

查看试题解析
14. 如图，在矩形ABCD中，把∠A沿DF折叠，点A恰好落在矩形的对称中心E处，则sin∠ADF的值为

查看试题解析
15. 如图，点A在双曲线y= $\frac{k}{x}$ （k＞0）上，过点A作AB⊥x轴，垂足为点B，分别以点O和点A为圆心，大于 $\frac{1}{2}$ OA的长为半径作弧，两弧相交于D，E两点，作直线DE交x轴于点C，交y轴于点F（0，2），连接AC.若AC=1，则k的值为.

查看试题解析
16. 如图，在Rt△ABC中，∠ACB＝90°，点D在AC上，DE⊥AB于点E，且CD＝DE.点F在BC上，连接EF，AF，若∠CEF＝45°，∠B＝2∠CAF，BF＝2，则AB的长为.

查看试题解析

三、解答题

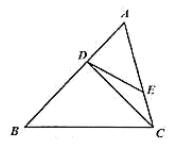
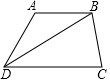
17. 计算：5x²•x⁴﹣（﹣2x³）²+x⁸÷x²

查看试题解析
18. 如图，四边形ABCD中，AB∥DC，AB＝AD，求证：BD平分∠ADC.

查看试题解析
19. 国家规定，“中小学生每天在校体育锻炼时间不小于1小时”，某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生，根据调查结果制作如下统计图（不完整）.其中分组情况：A组：时间小于0.5小时；B组：时间大于等于0.5小时且小于1小时；C组：时间大于等于1小时且小于1.5小时；D组：时间大于等于1.5小时.

根据以上信息，回答下列问题：

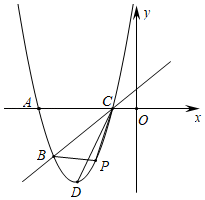
(1)、A组的人数是▲人，并补全条形统计图；

(2)、本次调查数据的中位数落在组；

(3)、根据统计数据估计该地区25 000名中学生中，达到国家规定的每天在校体育锻炼时间的人数约有多少人.

查看试题解析
20. 如图，△ABO是正三角形，CD∥AB，把△ABO绕△OCD的内心P旋转180°得到
△EFG

(1)、在图中画出点P和△EFG，保留画图痕迹，简要说明理由

(2)、若AO＝3 $\sqrt{3}$ ，CD＝2 $\sqrt{3}$ ，求A点运动到E点路径的长.

查看试题解析
21. 如图，AB是⊙O的直径，点C是⊙O上一点，AC平分∠DAB，直线DC与AB的延长线相交于点P，AD与PC延长线垂直，垂足为点D，CE平分∠ACB，交AB于点F，交⊙O于点E.

(1)、求证：PC与⊙O相切；

(2)、求证：PC＝PF；

(3)、若AC＝8，tan∠ABC＝ $\frac{4}{3}$ ，求线段BE的长.

查看试题解析
22. 鄂尔多斯市某百货商场销售某一热销商品A，其进货和销售情况如下：用16000元购进一批该热销商品A，上市后很快销售一空，根据市场需求情况，该商场又用7500元购进第二批该商品，已知第二批所购件数是第一批所购件数的一半，且每件商品的进价比第一批的进价少10元.

(1)、求商场第二批商品A的进价；

(2)、商场同时销售另一种热销商品B，已知商品B的进价与第二批商品A的进价相同，且最初销售价为165元，每天能卖出125件，经市场销售发现，若售价每上涨1元，其每天销售量就减少5件，问商场该如何定售价，每天才能获得最大利润？并求出每天的最大利润是多少？

查看试题解析
23. 如图，在 $Δ A B C$ 中，点 $D 、 E$ 分别在边 $A B$ 、 $A C$ 上，且 $A D = 3 ， A C = 6 ， A E = 4 ， A B = 8$ .

(1)、如果 $B C = 7$ ，求线段 $D E$ 的长；

(2)、设 $Δ D E C$ 的面积为 $a$ ，求 $Δ B D C$ 的面积（用 $a$ 的代数式表示）.

查看试题解析
24. 如图，已知抛物线 $y = a x^{2} + b x + 5$ 经过 $A (- 5，0)$ ， $B (- 4， - 3)$ 两点，与x轴的另一个交点为C，顶点为D，连结CD.

(1)、求该抛物线的表达式；

(2)、点P为该抛物线上一动点（与点B、C不重合），设点P的横坐标为t.
①当点P在直线BC的下方运动时，求 $Δ P B C$ 的面积的最大值；

②该抛物线上是否存在点P，使得 $∠ P B C = ∠ B C D$ 若存在，求出所有点P的坐标；若不存在，请说明理由.

查看试题解析