广西南宁市2020年数学中考二模试卷

试卷更新日期：2020-05-20 类型：中考模拟

进入出卷网下载

一、单选题

1. 在-2，-1，0，1这四个数中，最小的数是（）

A、-2 B、-1 C、0 D、1

查看试题解析
2. 某几何体的三视图如图所示，则下列说法错误的是（）

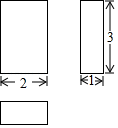A、该几何体是长方体 B、该几何体的高是3 C、底面有一边的长是1 D、该几何体的表面积为18平方单位

查看试题解析
3. 我国是一个干旱缺水严重的国家 $.$ 我国的淡水资源总量为28000亿立方米，占全球水资源的 $6 %$ ，仅次于巴西、俄罗斯和加拿大 $.$ 用科学记数法表示28000亿是 $($ 　　 $)$

A、 $2.8 \times 10^{4}$ B、 $28 \times 10^{3}$ C、 $28 \times 10^{11}$ D、 $2.8 \times 10^{12}$

查看试题解析
4. 如图，直线a，b被直线e，d所截，若∠1=∠2，∠3=125°，则∠4的度数为（）.

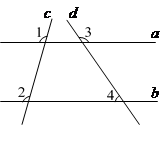A、55° B、60° C、70° D、75°

查看试题解析
5. 下列的调查中，选取的样本具有代表性的有 ( )

A、为了解某地区居民的防火意识，对该地区的初中生进行调查 B、为了解某校1200名学生的视力情况，随机抽取该校120名学生进行调查 C、为了解某商场的平均晶营业额，选在周末进行调查 D、为了解全校学生课外小组的活动情况，对该校的男生进行调查

查看试题解析
6. 下列运算正确的是（）

A、 $2 a \cdot 3 a^{2} = 6 a^{2}$ B、 ${(- a^{5})}^{2} = a^{10}$ C、 $- 2 a + a = 3 a$ D、 $- 6 a^{6} \div 2 a^{2} = - 3 a^{3}$

查看试题解析
7. 一个不透明的口袋中装有4个完全相同的小球，把它们分别标号为1，2，3，4，随机摸出一个小球后不放回，再随机摸出一个小球，则两次摸出的小球标号之和等于6的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{5}$ C、 $\frac{1}{4}$ D、 $\frac{1}{3}$

查看试题解析
8.
如图，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，若点A关于CD所在直线的对称点E恰好为AB的中点，则∠B的度数是（　　）

A、60° B、45° C、30° D、75°

查看试题解析
9. 下图是“明清影视城”的一扇圆弧形门，小红到影视城游玩，他了解到这扇门的相关数据：这扇圆弧形门所在的圆与水平地面是相切的， $A B = C D = 0.25$ 米， $B D = 1.5$ 米，且 $A B$ 、 $C D$ 与水平地面都是垂直的.根据以上数据，请你帮小红计算出这扇圆弧形门的最高点离地面的距离是（）

A、 $2$ 米 B、 $2.5$ 米 C、 $2.4$ 米 D、 $2.1$ 米

查看试题解析
10. 用长为4米的铝材制成一个矩形窗框，使它的面积为25平方米，若设它的一边长为 $x$ 米，根据题意列出关于 $x$ 的方程为（）

A、 $x (4 - x) = 25$ B、 $2 x (2 - x) = 25$ C、 $\frac{x (4 - 2 x)}{2} = 25$ D、 $\frac{x (2 - x)}{2} = 25$

查看试题解析
11. 已知，在河的两岸有A，B两个村庄，河宽为4千米，A，B两村庄的直线距离AB＝10千米，A，B两村庄到河岸的距离分别为1千米、3千米，计划在河上修建一座桥MN垂直于两岸，M点为靠近A村庄的河岸上一点，则AM+BN的最小值为（）

A、2 $\sqrt{13}$ B、1+3 $\sqrt{5}$ C、3+ $\sqrt{37}$ D、 $\sqrt{85}$

查看试题解析
12. 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动，第一次将点A向左移动3个单位长度到达点A₁ ，第二次将点A₁向右移动6个单位长度到达点A₂ ，第三次将点A₂向左移动9个单位长度到达点A₃ ， …按照这种移动规律进行下去，第51次移动到点 $A_{51}$ ，那么点A₅₁所表示的数为（　　）

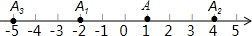A、﹣74 B、﹣77 C、﹣80 D、﹣83

查看试题解析

二、填空题

13. 若代数式 $\frac{x - 1}{x - 3}$ 有意义，则实数x的取值范围是．

查看试题解析

14. 某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核，甲、乙、丙各项得分如下表：

	笔试	面试	体能
甲	83	79	90
乙	85	80	75
丙	80	90	73

该公司规定：笔试、面试、体能得分分别不得低于80分、80分、70分，并按60%，30%，10%的比例计入总分，根据规定，可判定被录用.

查看试题解析

15. “手机阅读”已逐渐成了眼科病的主要病因，据调查表明在“中年人”中有“手机阅读”习惯的占比约达66%.若随机选择150名“中年人”进行调查，则估计有人有此习惯.

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $B C = 2$ ， $C D = \sqrt{3}$ ，以点 $B$ 为圆心， $B C$ 的长为半径作 $\overset{⌢}{C E}$ 交 $A D$ 于点 $E$ ；以点 $A$ 为圆心， $A E$ 的长为半径作 $\overset{⌢}{E F}$ 交 $A B$ 于点 $F$ ，则图中阴影部分的面积为.

查看试题解析
17. 如图，自左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第2个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成；…按照此规律，第n个图中正方形和等边三角形的个数之和为个．

查看试题解析
18. 如图，在直角三角形ABC中，∠A＝90°，AB＝8，AC＝15，BC＝17.D，P分别是线段AC，BC上的动点，则BD+DP的最小值是.

查看试题解析

三、解答题

19.

(1)、计算： $- \sqrt{18} + {(- 1)}^{2010} + 2 \sqrt{12} \times \frac{\sqrt{3}}{2} \div \sqrt{2}$

(2)、解方程： $x^{2} - 9 x + 8 = 0$ .

查看试题解析
20. 先化简( $\frac{3}{a + 1}$ －a＋1)÷ $\frac{a^{2} - 4 a + 4}{a + 1}$ ，并从0，－1，2中选一个合适的数作为a的值代入求值.

查看试题解析
21. 如图，在平面直角坐标系中， $△ ABC$ 的三个顶点分别为 $A (- 4 ， 0)$ ， $B (- 3 ， - 3)$ ， $C (- 1 ， - 3)$ .

①将 $△ ABC$ 向右平移6个单位后得到 $△ A_{1} B_{1} C_{1}$ ，请在图中画出 $△ A_{1} B_{1} C_{1}$ ，并写出 $C_{1}$ 点坐标；

②图中点 $B_{2} (1 ， 1)$ 与点B关于直线l成轴对称，请在图中画出直线l及 $△ ABC$ 关于直线l对称的 $△ A_{2} B_{2} C_{2}$ ，并直接写出直线l对应的函数关系式.

查看试题解析
22. 某中学团委会开展书法、诵读、演讲、征文四个项目（每人只参加一个项目）的比赛，初三（1）班全体同学都参加了比赛，为了解比赛的具体情况，小明收集整理数据后，绘制了以下不完整的折线统计图和扇形统计图，根据图表中的信息解答下列各题：

(1)、初三（1）班的总人数为，扇形统计图中“征文”部分的圆心角度数为度；

(2)、请把折线统计图补充完整；

(3)、平平和安安两个同学参加了比赛，请用“列表法”或“画树状图法”，求出他们参加的比赛项目相同的概率．

查看试题解析
23. 如图，在 $⊙ O$ 中，直径 $A B$ 平分弦 $C D$ 、 $A B$ 与 $C D$ 相交于点 $E$ ，连接 $A C$ 、 $B C$ ，点 $F$ 是 $B A$ 延长线上的一点，且 $∠ F C A = ∠ B$ .

(1)、求证： $C F$ 是 $⊙ O$ 的切线.

(2)、若 $A C = 4$ ， $\frac{A E}{E C} = \frac{1}{2}$ ，求 $⊙ O$ 的半径.

查看试题解析

24. 某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如表：

	原进价（元/张）	零售价（元/张）	成套售价（元/套）
餐桌	a	270	500元
餐椅	a﹣110	70	500元

已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.

(1)、求表中a的值；

(2)、若该商场购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套（一张餐桌和四张餐椅配成一套）销售，其余餐桌、餐椅以零售方式销售.请问怎样进货，才能获得最大利润？最大利润是多少？

(3)、由于原材料价格上涨，每张餐桌和餐椅的进价都上涨了10元，但销售价格保持不变.商场购进了餐桌和餐椅共200张，应怎样安排成套销售的销售量（至少10套以上），使得实际全部售出后，最大利润与（2）中相同？请求出进货方案和销售方案.

查看试题解析

25. 如图， $Δ A B C$ 是 $⊙ O$ 的内接三角形， $∠ B A C$ 的角平分线 $A E$ 交 $⊙ O$ 于点 $E$ ，交 $B C$ 于点 $D$ ，过点 $E$ 作直线 $l // B C$ .

(1)、判断直线 $l$ 与 $⊙ O$ 的位置关系，并说明理由；

(2)、若在 $A E$ 上取一点 $F$ 使 $E F = B E$ ，求证： $B F$ 是 $∠ A B C$ 的平分线；

(3)、在（2）的条件下，若 $D E = 3$ ， $B E = 5$ ，求 $A E$ 的长.

查看试题解析
26. 如图，抛物线 $y = - x^{2} + bx + c$ 与 $x$ 轴交于 $A (- 7 ， 0)$ ， $B (1 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ，抛物线的对称轴与 $x$ 轴交于点 $D$ ，顶点坐标为 $M$ .

(1)、求抛物线的表达式和顶点 $M$ 的坐标；

(2)、如图1，点 $E (x ， y)$ 为抛物线上一点，点 $E$ 不与点 $M$ 重合，当 $- 7 < x < - 2$ 时，过点 $E$ 作 $EF / / x$ 轴，交抛物线的对称轴于点 $F$ ，作 $EH ⊥ x$ 轴于点H，得到矩形 $EHDF$ ，求矩形 $EHDF$ 的周长的最大值；

(3)、如图2，点 $P$ 为抛物线对称轴上一点，是否存在点 $P$ ，使以点 $P$ 、 $A$ 、 $C$ 为顶点的三角形是直角三角形？若存在，求出点 $P$ 的坐标；若不存在，请说明理由.

查看试题解析