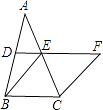新疆昌吉市教育共同体2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-05-19 类型:期中考试
一、单选题
-
1. 下列式子为最简二次根式的是( )
A、 B、 C、 D、2. 满足下列条件的三角形中,不是直角三角形的是( )A、三内角之比为1:2:3 B、三边长之比为3:4:5 C、三边长分别为1, , D、三边长分别为5,12,143. 正方形具有而菱形不一定具有的性质是( )A、四边相等 B、对角线相等 C、对角相等 D、对角线互相垂直4. 如果 ,则a的取值范围是( )A、 B、 C、 D、5. 已知矩形ABCD,AB=2BC,在CD上取点E,使AE=EB,那么∠EBC等于( )A、15° B、30° C、45° D、60°6. 平行四边形的一条边长是12cm,那么它的两条对角线的长可能是( )
A、8cm和16cm B、10cm和16cm C、8cm和14cm D、8cm和12cm7. 如图,A,B两地被池塘隔开,小康通过下列方法测出了A,B间的距离:先在AB外选一他点C,然后测出AC,BC的中点M、N,并测量出MN的长为18m,由此他就知道了A,B间的距离.下列有关他这次探究活动的结论中,错误的是( ) A、AB=36m B、MN∥AB C、MN=C D、CM= AC8. 下列计算中,正确的是( )A、5 B、 (a>0,b>0) C、 D、9. 一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为( )
A、AB=36m B、MN∥AB C、MN=C D、CM= AC8. 下列计算中,正确的是( )A、5 B、 (a>0,b>0) C、 D、9. 一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为( )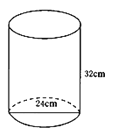 A、20cm B、50cm C、40cm D、45cm10. 如图,设M是▱ABCD一边上任意一点,设△AMD的面积为S1 , △BMC的面积为S2 , △CDM的面积为S,则( )
A、20cm B、50cm C、40cm D、45cm10. 如图,设M是▱ABCD一边上任意一点,设△AMD的面积为S1 , △BMC的面积为S2 , △CDM的面积为S,则( ) A、S=S1+S2 B、S>S1+S2 C、S<S1+S2 D、不能确定11. 如图,▱ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A、S=S1+S2 B、S>S1+S2 C、S<S1+S2 D、不能确定11. 如图,▱ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( ) A、BE=DF B、BF=DE C、AE=CF D、∠1=∠212. 已知n是一个正整数, 是整数,则n的最小值是( ).A、3 B、5 C、15 D、2513. 如图,四边形ABCD是菱形,对角线AC=8,DB=6,DH⊥AB于点H,则DH的长为( )
A、BE=DF B、BF=DE C、AE=CF D、∠1=∠212. 已知n是一个正整数, 是整数,则n的最小值是( ).A、3 B、5 C、15 D、2513. 如图,四边形ABCD是菱形,对角线AC=8,DB=6,DH⊥AB于点H,则DH的长为( ) A、4.8cm B、5cm C、9.6cm D、10cm14.
A、4.8cm B、5cm C、9.6cm D、10cm14.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
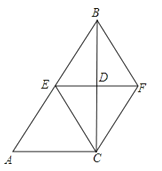 A、BC=AC B、CF⊥BF C、BD=DF D、AC=BF15. 如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( )
A、BC=AC B、CF⊥BF C、BD=DF D、AC=BF15. 如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( ) A、3 B、 C、5 D、
A、3 B、 C、5 D、二、填空题
-
16. 命题“菱形的四条边都相等”的逆命题是.17. 如图,数轴上点A表示的实数是 .
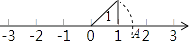 18. 如图,在Rt△ABC中,E是斜边AB的中点,若AB=10,则CE= .
18. 如图,在Rt△ABC中,E是斜边AB的中点,若AB=10,则CE= . 19. 已知a,b是正整数,若 + 是不大于2的整数,则满足条件的有序数对(a,b)为 .20. 如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于点F,EG⊥BD于点G,则EF+EG=.
19. 已知a,b是正整数,若 + 是不大于2的整数,则满足条件的有序数对(a,b)为 .20. 如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于点F,EG⊥BD于点G,则EF+EG=.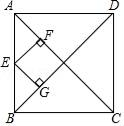
三、解答题
-
21. 计算:(1)、 ;(2)、 .22. 如图,正方形网格中每个小正方形的边长为1,试回答问题:∠BCD是直角吗?说明理由.
 23. 如图,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC,交BC于F,试说明EC=EF=BF.
23. 如图,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC,交BC于F,试说明EC=EF=BF. 24. 已知x= +1,y= ﹣1,求下列各代数式的值:(1)、x2y﹣xy2;(2)、x2﹣xy+y2.25. 如图,在四边形ABCD中,AB∥CD,AD∥BC,AN=CM.
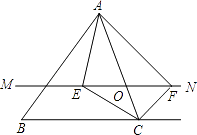
24. 已知x= +1,y= ﹣1,求下列各代数式的值:(1)、x2y﹣xy2;(2)、x2﹣xy+y2.25. 如图,在四边形ABCD中,AB∥CD,AD∥BC,AN=CM. (1)、求证:BN=DM;(2)、若BC=3,CD=2,∠B=50°,求∠BCD、∠D的度数及四边形ABCD的周长.26. 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,某一时刻,AC=18 km,且OA=OC.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为40km/h和30km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D处,求此时B处距离D处多远?
(1)、求证:BN=DM;(2)、若BC=3,CD=2,∠B=50°,求∠BCD、∠D的度数及四边形ABCD的周长.26. 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,某一时刻,AC=18 km,且OA=OC.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为40km/h和30km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D处,求此时B处距离D处多远?