广东省佛山市顺德区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-05-19 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形不是轴对称图形的是（　　）

A、线段 B、角 C、直角三角形 D、等腰三角形

查看试题解析
2. 数0.000075用科学记数法表示为（　　）

A、7.5×10⁵ B、75×10^﹣4 C、7.5×10^﹣5 D、75×10^﹣5

查看试题解析
3. 下列运算正确的是（　　）

A、m²•m³＝m⁵ B、（mn）²＝mn² C、（m³）²＝m⁹ D、m⁶÷m²＝m³

查看试题解析
4. 已知∠A＝40°，那么∠A的补角的度数等于（　　）

A、50° B、60° C、140° D、150

查看试题解析
5. 整式的乘法计算正确的是（　　）

A、（x+3）（x﹣3）＝x²+3 B、（x+y）²＝x²+y² C、6x²• $\frac{1}{2} x^{3}$ ＝3x⁶ D、（2x+y）（x﹣y）＝2x²﹣xy﹣y²

查看试题解析
6. 以每组数为线段的长度，可以构成三角形三边的是（）

A、 $13$ 、 $12$ 、 $20$ B、 $7$ 、 $8$ 、 $15$ C、 $7$ 、 $2$ 、 $4$ D、 $5$ 、 $5$ 、 $11$

查看试题解析
7. 下列变形正确的是（　　）

A、10a⁴b³÷5a²b＝2a²b³ B、（﹣bc）⁴÷（﹣bc）²＝﹣b²c² C、（3xy+y）÷y＝3x+y D、 $a^{- p} = \frac{1}{a^{p}}$ （a≠0，P是正整数）

查看试题解析
8. 直线a、b被c、d所截．若∠1＝80°，∠2＝100°，下列结论不正确的是（　　）

A、a∥b B、∠3+∠4＝180° C、∠3＝∠4 D、∠5＝80°

查看试题解析
9. 如图，在四边形ABCD中，AB∥CD，不能判定△ABD≌△CDB的条件是（　　）

A、AB＝CD B、AD＝BC C、AD∥BC D、∠A＝∠C

查看试题解析
10. 如图是一辆汽车行驶的速度（千米/时）与时间（分）之间变化图，下列说法正确的是（）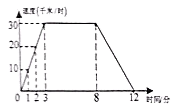

A、时间是因变量，速度是自变量 B、从 $3$ 分到 $12$ 分，汽车行驶的路程是 $150$ 千米 C、时间每增加 $1$ 分钟，汽车的速度增加 $10$ 千米时 D、第 $3$ 分钟时汽车的速度是 $30$ 千米/时

查看试题解析

二、填空题（6个题，每题4分，共24分）

11. 计算：（﹣2）²×2³＝．

查看试题解析
12. 计算：（x﹣1）²＝．

查看试题解析

13. 对某批乒乓球的质量进行随机抽查，结果如下表所示：

随机抽取的乒乓球数 $n$	$10$	$20$	$50$	$100$	$200$	$500$	$1000$
优等品数 $m$	$7$	$16$	$43$	$81$	$164$	$414$	$824$
优等品率 $\frac{m}{n}$	$0.7$	$0.8$	$0.86$	$0.81$	$0.82$	$0.828$	$0.824$

当 $n$ 越大时，优等品率趋近于概率．（精确到 $0.01$ ）

查看试题解析

14. 在一次实验中，A同学把一根弹簧的上端固定，在其下端悬挂物体，测弹簧长度y（cm）随所挂物体的质量x（kg）变化关系如下表：

x（kg）

0

1

2

3

4

5

y（cm）

8

10

12

14

16

18

根据表格中数据写出y与x关系式：．

查看试题解析
15. 在直角三角形中，一个锐角比另一个锐角的3倍还多10°，则较小的锐角度数是．

查看试题解析
16. 如图，在△ABC中，AC＝BC，∠C＝90°，AD是∠BAC的平分线，折叠△ACD使得点C落在AB边上的E处，连接DE、CE．下列结论：①∠CAD＝∠EAD；②△CDE是等腰三角形；③AD⊥CE；④AB＝AC+CD，其中正确的结论是．（填写序号）

查看试题解析

三、解答题（一）

17. 计算： ${(- 1)}^{2009} + {(\frac{1}{2})}^{- 1} - {(3.14 - π)}^{0} + | - 4 |$

查看试题解析
18. 先化简，再求值：[（x+2y）²﹣（x+y）（x﹣y）]÷(2y)，其中x＝ $\frac{1}{2}$ ，y＝﹣2．

查看试题解析
19. 如图，Rt△ABC中，∠A＝90°．

(1)、用尺规作图法作∠ABD＝∠C，与边AC交于点D（保留作图痕迹，不用写作法）；

(2)、在（1）的条件下，当∠C＝30°时，求∠BDC的度数．

查看试题解析

四、解答题（二）

20. 某路口南北方向红绿灯的设置时间为：红灯40s、绿灯60s、黄灯3s．司机A随机地由南往北开车到达该路口，问：

(1)、他遇到红灯的概率大还是遇到绿灯的概率大？

(2)、他遇到绿灯的概率是多少？

查看试题解析
21. 如图，一条输电线路需跨越一个池塘，池塘两侧A、B处各立有一根电线杆，但利用皮尺无法直接量出A、B间的距离．请设计一个方案测出A、B间的距离，要求画出方案的几何图形，并说明理由．

查看试题解析
22. 如图，AC与BD相交于点E，AB＝CD，∠A＝∠D．

(1)、试说明△ABE≌△DCE；

(2)、连接AD，判断AD与BC的位置关系，并说明理由．

查看试题解析

五、解答题（三）

23. 已知A＝x³÷x²+x•x² ， B＝（x+1）²﹣（x﹣1）²

(1)、求A•B；

(2)、若变量y满足4A÷B﹣2y＝0，用x表示变量y，并求出x＝﹣2时y的值；

(3)、若A＝B+1，求x⁵﹣x²﹣9x+5的值．

查看试题解析
24. 如图，在△ABC中，AB＝AC，AD是中线，作AD关于AC的轴对称图形AE．

(1)、直接写出AC和DE的位置关系．

(2)、连接CE，写出BD和CE的数量关系，并说明理由；

(3)、当∠BAC＝90°，BC＝8时，在AD上找一点P，使得点P到点C与到点E的距离之和最小，求△BCP的面积．

查看试题解析
25. 已知，AB＝18，动点P从点A出发，以每秒1个单位的速度向点B运动，分别以AP、BP为边在AB的同侧作正方形．设点P的运动时间为t．

(1)、如图1，若两个正方形的面积之和S，当t＝6时，求出S的大小；

(2)、如图2，当t取不同值时，判断直线AE和BC的位置关系，说明理由；

(3)、如图3，用t表示出四边形EDBF的面积y．

查看试题解析

x（kg）	0	1	2	3	4	5
y（cm）	8	10	12	14	16	18