广东省茂名市电白区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-05-19 类型:期末考试
一、选择题(共10小题,每小题3分,满分30分)
-
1. 计算6m3÷(﹣3m2)的结果是( )A、﹣3m B、﹣2m C、2m D、3m2. 下列各组长度的三条线段能组成三角形的是( )A、5cm,3cm,9cm B、5cm,3cm,8cm C、5cm,3cm,7cm D、6cm,4cm,2cm3. 用科学记数法表示0.0000907,得( )A、9.07×10﹣4 B、9.07×10﹣6 C、9.07×105 D、9.07×10﹣54. 如果两个不相等的角互为补角,那么这两个角( )A、都是锐角 B、都是钝角 C、一个锐角,一个钝角 D、以上答案都不对5. 数学课上老师给出了下面的数据,请问哪一个数据是精确的( )A、2003年美国发动的伊拉克战争每月耗费约40亿美元 B、地球上煤储量为5万亿吨左右 C、人的大脑约有1×1010个细胞 D、某次期中考试中小颖的数学成绩是98分6. 如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需再有下列条件中的( )即可.
 A、∠1=∠2 B、∠1=∠DFE C、∠1=∠AFD D、∠2=∠AFD7. 如图,若AB=AC,BE=CF,CF⊥AB,BE⊥AC,则图中全等的三角形共有( )对.
A、∠1=∠2 B、∠1=∠DFE C、∠1=∠AFD D、∠2=∠AFD7. 如图,若AB=AC,BE=CF,CF⊥AB,BE⊥AC,则图中全等的三角形共有( )对. A、5对 B、4对 C、3对 D、2对8. 利用基本作图,不能作出唯一三角形的是( )A、已知两边及其夹角 B、已知两角及夹边 C、已知两边及一边的对角 D、已知三边9. 如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图象是( )
A、5对 B、4对 C、3对 D、2对8. 利用基本作图,不能作出唯一三角形的是( )A、已知两边及其夹角 B、已知两角及夹边 C、已知两边及一边的对角 D、已知三边9. 如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图象是( ) A、
A、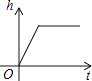 B、
B、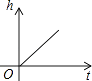 C、
C、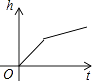 D、
D、 10. 如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
10. 如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( ) A、∠DAB′=∠CAB′ B、∠ACD=∠B′CD C、AD=AE D、AE=CE
A、∠DAB′=∠CAB′ B、∠ACD=∠B′CD C、AD=AE D、AE=CE二、填空题
-
11. ﹣ 的系数是 , 次数是 .12. 一个两位数,个位上的数字是a,十位上的数字是b,交换这个两位数个位上与十位上数的位置,得到新的两位数,这两个两位数的和是 .13. 等边三角形有条对称轴,矩形有条对称轴.14. 如图,要使AB∥CD,只需要添加一个条件,这个条件是(填一个你认为正确的条件即可).
 15. 如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是 .
15. 如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是 . 16. 如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN∥BC,MN过点O.若AB=12,AC=18,则△AMN的周长是 .
16. 如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN∥BC,MN过点O.若AB=12,AC=18,则△AMN的周长是 .
三、解答题(共3小题,满分18分)
-
17. 计算:4(x﹣y)2﹣(2x﹣y)(2x+y)18. 已知:如图,AB∥EF,BC∥ED,AB,DE交于点G.
求证:∠B=∠E.
 19. 如图,在△ABC和△BAD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:∠1=∠2.
19. 如图,在△ABC和△BAD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:∠1=∠2.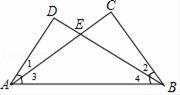
四、简答题(每小题7分,共21分)
-
20. 如图,为了测量出池塘两端A、B之间的距离,先在地面上取一点C,使∠ACB=90°,然后延长BD至D,使CD=BC,那么只要测量出AD的长度就得到A,B两点之间的距离,你能说明其中的道理吗?
 21. 已知∠AOB及射线OA边上的点M(如图),请用尺规过点M作OB的平行线EF,不写作法,保留作图痕迹.
21. 已知∠AOB及射线OA边上的点M(如图),请用尺规过点M作OB的平行线EF,不写作法,保留作图痕迹.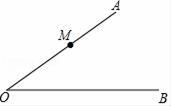 22. 如图所示,转盘被等分成六个扇形,并在上面一次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求:
22. 如图所示,转盘被等分成六个扇形,并在上面一次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求: (1)、指针指向4的概率;(2)、指针指向数字是奇数的概率;(3)、指针指向数字不小于5的概率.
(1)、指针指向4的概率;(2)、指针指向数字是奇数的概率;(3)、指针指向数字不小于5的概率.五、简答題(每小题9分,共27分)
-
23. 如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
 (1)、求出△ABC的面积(2)、在图中作出△ABC关于y轴的对称图形△A1B1C1(3)、写出点A1 , B1 , C1的坐标24. “珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)、求出△ABC的面积(2)、在图中作出△ABC关于y轴的对称图形△A1B1C1(3)、写出点A1 , B1 , C1的坐标24. “珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题: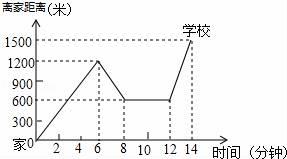 (1)、小明家到学校的路程是多少米?(2)、小明在书店停留了多少分钟?(3)、本次上学途中,小明一共行驶了多少米?一共用了多少分钟?(4)、我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?25. 已知:如图:△ABC是等边三角形,点D、E分别是边BC、CA上的点,且BD=CE,AD、BE相交于点O.
(1)、小明家到学校的路程是多少米?(2)、小明在书店停留了多少分钟?(3)、本次上学途中,小明一共行驶了多少米?一共用了多少分钟?(4)、我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?25. 已知:如图:△ABC是等边三角形,点D、E分别是边BC、CA上的点,且BD=CE,AD、BE相交于点O. (1)、求证:△ACD≌△BAE;(2)、求∠AOB的度数.
(1)、求证:△ACD≌△BAE;(2)、求∠AOB的度数.