广东省广州市越秀区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-05-19 类型：期末考试

进入出卷网下载

一、选择题（共10小题，每小题3分，满分30分）

1. 在平面直角坐标系中，已知点P（﹣2，3），则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列说法不正确的是（　　）

A、0的立方根是0 B、0的平方根是0 C、1的立方根是±1 D、4的平方根是±2

查看试题解析
3. 如图，下列判断中正确的是（　　）

A、如果∠3+∠2＝180°，那么AB∥CD B、如果∠1+∠3＝180°，那么AB∥CD C、如果∠2＝∠4，那么AB∥CD D、如果∠1＝∠5，那么AB∥CD

查看试题解析
4. 如图，下列判断中正确的是（　　）

A、如果EF∥GH，那么∠4+∠3＝180° B、如果∠1+∠3＝180°，那么AB∥CD C、如果∠2＝∠4，那么AB∥CD D、如果∠1＝∠2，那么AB∥CD

查看试题解析
5. 在下列四项调查中，方式正确的是 $($ $)$

A、了解本市中学生每天学习所用的时间，采用全面调查的方式 B、为保证运载火箭的成功发射，对其所有的零部件采用抽样调查的方式 C、了解某市每天的流动人口数，采用全面调查的方式 D、了解全市中学生的视力情况，采用抽样调查的方式

查看试题解析
6. 为了了解某校七年级学生的体能情况，随机调查了其中100名学生，测试学生在1分钟内跳绳的次数，并绘制成如图所示的频数分布直方图．请根据图形计算，跳绳次数（x）在120≤x＜200范围内人数占抽查学生总人数的百分比为（　　）

A、43% B、50% C、57% D、73%

查看试题解析
7. 实数a、b在数轴上的位置如图所示，则下列各式表示正确的是（　　）

A、b﹣a＜0 B、1﹣a＞0 C、b﹣1＞0 D、﹣1﹣b＜0

查看试题解析
8. 已知﹣1＜x＜0，那么在x、2x、 $\sqrt{(- x)}$ 、﹣x²中最小的数是（　　）

A、﹣x² B、2x C、 $\sqrt{(- x)}$ D、x

查看试题解析
9. 不等式组 ${\begin{matrix} 5 x - 3 < 3 x + 5 \\ x < a \end{matrix}$ 的解集为x＜4，则a满足的条件是（）

A、a＜4 B、a=4 C、a≤4 D、a≥4

查看试题解析
10. 若满足方程组 ${\begin{cases} 3 x + y = m + 3 \\ 2 x - y = 2 m - 1 \end{cases}$ 的x与y互为相反数，则m的值为（　　）

A、1 B、﹣1 C、11 D、﹣11

查看试题解析

二、填空题（共有6小题，每小题3分，共18分）

11. 已知A（2，﹣3），先将点A向左平移3个单位，再向上平移2个单位得到点B，则点B的坐标是．

查看试题解析
12. 如图，已知AB⊥CD，垂足为点O，直线EF经过O点，若∠1＝55°，则∠COE的度数为度．

查看试题解析
13. 在扇形统计图中，其中一个扇形所表示的部分占总体的30%，则这个扇形的圆心角是度．

查看试题解析
14. 已知（a﹣1）²+|b+1|+ $\sqrt{b + c - a}$ ＝0，则a+b+c＝．

查看试题解析
15. 已知直线AB∥x轴，A点的坐标为（1，2），并且线段AB＝3，则点B的坐标为．

查看试题解析
16. 我们规定：相等的实数看作同一个实数．有下列六种说法：
①数轴上有无数多个表示无理数的点；

②带根号的数不一定是无理数；

③每个有理数都可以用数轴上唯一的点来表示；

④数轴上每一个点都表示唯一一个实数；

⑤没有最大的负实数，但有最小的正实数；

⑥没有最大的正整数，但有最小的正整数．

其中说法不正确的有（注：填写出所有不正确说法的编号）

查看试题解析

三、解答题（本题共有7小题，共72分）

17. 如图，点B、E分别在直线AC和DF上，若∠AGB＝∠EHF，∠C＝∠D，可以证明∠A＝∠F．请完成下面证明过程中的各项“填空”．
证明：∵∠AGB＝∠EHF（理由：）

∠AGB＝（对顶角相等）

∴∠EHF＝∠DGF，∴DB∥EC（理由：）

∴∠＝∠DBA（两直线平行，同位角相等）

又∵∠C＝∠D，∴∠DBA＝∠D，

∴DF∥（内错角相等，两直线平行）

∴∠A＝∠F（理由：）．

查看试题解析
18.

(1)、解方程组 ${\begin{cases} 4 (x + 3) + 5 (y - 1) = 0 ① \\ 2 x + 3 (y + 2) = 3 ② \end{cases}$

(2)、解方程组 ${\begin{cases} \frac{x- 3}{2} = \frac{y + 1}{3} ① \\ \frac{2}{3} (x - 1) + \frac{y}{3} = 1 ② \end{cases}$ ；

(3)、解不等式组 ${\begin{cases} x - 3 (x - 2) \geq 4 ① \\ \frac{2 x - 1}{2} + 1 \geq \frac{x + 1}{2} ② \end{cases}$ ．

查看试题解析
19. 某中学改革学生的学习模式，变“老师要学生学习”为“学生自主学习”，培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学，根据收集到的数据绘制了以下两个不完整的统计图（如图）.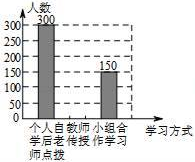

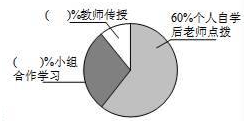
请根据上面两个不完整的统计图回答以下4个问题：

(1)、这次抽样调查中，共调查了名学生.

(2)、补全条形统计图中的缺项.

(3)、在扇形统计图中，选择教师传授的占%，选择小组合作学习的占%.

(4)、根据调查结果，估算该校1800名学生中大约有人选择小组合作学习模式.

查看试题解析
20. 如图，EF∥AD，∠1＝∠2，∠BAC＝80°．求∠AGD的度数．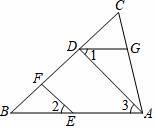

查看试题解析
21. 在下列网格中建立平面直角坐标系如图，每个小正方形的边长均为1个单位长度．已知A（1，1）、B（3，4）和C（4，2）．

(1)、在图中标出点A、B、C．

(2)、将点C向下平移3个单位到D点，将点A先向左平移3个单位，再向下平移1个单位到E点，在图中标出D点和E点．

(3)、求△EBD的面积S_△EBD ．

查看试题解析
22. 某公司组织退休职工组团前往某景点游览参观，参加人员共70人．旅游景点规定：①门票每人60元，无优惠；②上山游览必须乘坐景点安排的观光车游览，观光车有小型车和中型车两类，分别可供4名和11名乘客乘坐；且小型车每辆收费60元，中型车每人收费10元．若70人正好坐满每辆车且参观游览的总费用不超过5000元，问景点安排的小型车和中型车各多少辆？

查看试题解析
23. 某工厂现有甲种原料3600kg，乙种原料2410kg，计划利用这两种原料生产A，B两种产品共500件，产品每月均能全部售出．已知生产一件A产品需要甲原料9kg和乙原料3kg；生产一件B种产品需甲种原料4kg和乙种原料8kg．

(1)、设生产x件A种产品，写出x应满足的不等式组．

(2)、问一共有几种符合要求的生产方案？并列举出来．

(3)、若有两种销售定价方案，第一种定价方案可使A产品每件获得利润1.15万元，B产品每件获得利润1.25万元；第二种定价方案可使A和B产品每件都获得利润1.2万元；在上述生产方案中哪种定价方案盈利最多？（请用数据说明）

查看试题解析