广东省佛山市南海区里水镇2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期：2020-05-19 类型：期末考试
一、选择题
-
1. 某次地震导致地球当天自转快了0.0000016秒．这里的0.0000016用科学记数法表示为（ ）A、16×10﹣7 B、1.6×10﹣5 C、1.6×10﹣6 D、0.16×10﹣52. 计算（x2y）2的结果是（ ）A、x4y2 B、x4y C、x2y2 D、x2y3. 下列计算正确的是（ ）A、a4+a2＝a6 B、a5•a2＝a7 C、（ab5）2＝ab10 D、a10÷a2＝a54. 下列各图中，∠1与∠2互为余角的是（ ）A、
B、
C、
D、
5. 下列是平方差公式应用的是（ ）A、（x+y）（﹣x﹣y） B、（2a﹣b）（2a+b） C、（﹣m+2n）（m﹣2n） D、（4x+3y）（4y﹣3x）6. 以下列各组线段长为边，能组成三角形的是（ ）
A、2，2，4 B、2，6，3 C、12，5，6 D、7，3，67. 如图，直线l1∥l2 ， 且分别与直线l交于C ， D两点，把一块含30°角的三角尺按如图所示的位置摆放，若∠1＝58°，则∠2的度数为（ ）
A、92° B、98° C、102° D、122°8. 如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（ ）
A、∠3＝∠A B、∠1＝∠2 C、∠D＝∠DCE D、∠D+∠ACD＝180°9. 周末小丽从家里出发骑单车去公园，因为她家与公园之间是一条笔直的自行车道，所以小丽骑得特别放松．途中，她在路边的便利店挑选一瓶矿泉水，耽误了一段时间后继续骑行，愉快地到了公园．图中描述了小丽路上的情景，下列说法中不正确的是（ ）
A、小丽在便利店时间为15分钟 B、公园离小丽家的距离为2000米 C、小丽从家到达公园共用时间20分钟 D、小丽从家到便利店的平均速度为100米/分钟10. 如图，已知AB＝AC，AF＝AE，∠EAF＝∠BAC，点C、D、E、F共线．则下列结论，其中正确的是（ ）
①△AFB≌△AEC；②BF＝CE；③∠BFC＝∠EAF；④AB＝BC．
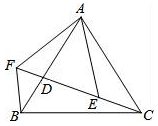A、①②③ B、①②④ C、①② D、①②③④二、填空题
-
11. 若2x＝5，2y＝3，则2x+y＝ ．12. 如图所示，AB＝AD，∠1＝∠2，在不改变图形的情况下，请你添加一个条件，使△ABC≌△ADE，则需添加的条件是 ．
13. 如图，在立定跳远后，体育老师是这样测量运动员的成绩的，用一块直角三角板的一边附在跳线上，另一边与拉的皮尺重合，这样做的理由是 ．
14. 若（x+y）2＝49，xy＝12，则x2+y2＝ ．15. 已知AD是△ABC的高，∠BAD=72°，∠CAD=21°，则∠BAC的度数是.16. 将一张长方形纸片按图中方式折叠，若∠2＝65°，则∠1的度数为 ．
三、解答题（一）
-
17. 计算： + ﹣ ．18. 先化简，再求值[（2x+y）（2x﹣y）﹣（2x﹣3y）2]÷2y，其中x＝2，y＝119. 已知：如图，在△ABC中，∠BAC＝80°，AD⊥BC于D，AE平分∠DAC，∠B＝60°；求∠AEC的度数．
四、解答题（二）
-
20. 如图，在射线BC上取一点A，以AC为一边作∠CAD．
(1)、以B为顶点，用直尺和圆规作∠CBE，使得∠CBE＝∠CAD；(2)、在所作的图中，BE与AD平行吗？为什么？21. 生活中处处有数字，只要同学们学会数学的眼光观察生活，就会有许多意想不到的收获，如图两幅图都是由同一副三角板拼凑得到的．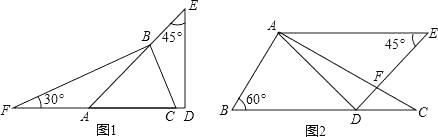
(1)、图1中的∠ABC的度数是多少？
(2)、图2中已知AE∥BC，则∠AFD的度数是多少？
22. 如图，已知AD∥BC一点E为CD上一点，AE、BE分别平分∠DAB、∠CBA，BE交AD的延长线于点F．
(1)、求证：△ABE≌△AFE；(2)、求证：AD+BC＝AB．五、解答题（三）（本大题3小题，每小题9分，共27分）
-
23. “龟兔赛跑”的故事同学们都非常熟悉，图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．
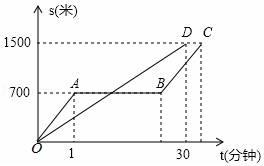(1)、填空：折线OABC表示赛跑过程中的路程与时间的关系，线段OD表示赛跑过程中的路程与时间的关系．赛跑的全程是米．(2)、兔子在起初每分钟跑多少米？乌龟每分钟爬多少米？(3)、乌龟用了多少分钟追上了正在睡觉的兔子？(4)、兔子醒来，以48千米/时的速度跑向终点，结果还是比乌龟晚到了0.5分钟，请你算算兔子中间停下睡觉用了多少分钟？24.
(1)、如图1，阴影部分的面积是 ． （写成平方差的形式）(2)、若将图1中的阴影部分剪下来，拼成如图2的长方形，面积是 ． （写成多项式相乘的积形式）(3)、比较两图的阴影部分的面积，可以得到公式： ．(4)、应用公式计算：（1﹣ ）（1﹣ ）（1﹣ ）（1﹣ ）…（1﹣ ）（1﹣ ）．25. 如图1，△ABC和△DBE是等腰直角三角形，且∠ABC＝∠DBE＝90°，D点在AB上，连接AE与CD的延长线交于点F，
(1)、直接写出线段AE与CD的数量关系．(2)、若将图1中的△DBE绕点B逆时针旋转一个锐角，如图2所示，问图2中的线段AE、CD之间有怎样的数量和位置关系？(3)、拓展：若将图1中的△DBE绕点B逆时针旋转一个锐角，将“∠ABC＝∠DBE＝90°”改为“∠ABC＝∠DBE＝α（α为锐角）”，其他条件均不变，如图3所示，问：线段AE、CD所在直线的夹角大小是否随着图形的旋转而发生变化？若不变，其值多少？