吉林省长春市汽开区2018-2019学年八年级下学期期末考试试卷
试卷更新日期:2020-05-18 类型:期末考试
一、选择题
-
1. 在平面直角坐标系中,若点 的坐标为 ,则点 在( )A、第一象限. B、第二象限. C、第三象限 D、第四象限2. 计算 的结果是( )A、 B、2 C、1 D、-53. 环保部门根据我市 一周的检测数据列出下表.这组数据的中位数是( )
 A、 B、 C、 D、4. 下列函数的图象经过(0,1),且y随x的增大而减小的是( )A、y=一x B、y=x-1 C、y=2x+1 D、y=一x+15. 如图,在▱ABCD中,对角线AC、BD交于点O.若AC=4,BD=5,BC=3,则△BOC的周长为( )
A、 B、 C、 D、4. 下列函数的图象经过(0,1),且y随x的增大而减小的是( )A、y=一x B、y=x-1 C、y=2x+1 D、y=一x+15. 如图,在▱ABCD中,对角线AC、BD交于点O.若AC=4,BD=5,BC=3,则△BOC的周长为( )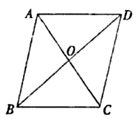 A、6 B、7.5 C、8 D、126. 若一次函数 的图象如图所示,则不等式 的解集为( )
A、6 B、7.5 C、8 D、126. 若一次函数 的图象如图所示,则不等式 的解集为( )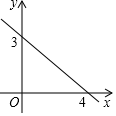 A、 B、 C、 D、7. 如图,在正方形 中,以点 为圆心,以 长为半径画圆弧,交对角线 于点 ,再分别以点 、 为圆心,以大于 长为半径画圆弧,两弧交于点 ,连结 并延长,交 的延长线于点 ,则 的大小为( )
A、 B、 C、 D、7. 如图,在正方形 中,以点 为圆心,以 长为半径画圆弧,交对角线 于点 ,再分别以点 、 为圆心,以大于 长为半径画圆弧,两弧交于点 ,连结 并延长,交 的延长线于点 ,则 的大小为( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,点A、B的坐标分别是(4,0)、(0,3),点O'在直线y=2x(x≥0)上,将△AOB沿射线OO'方向平移后得到△A'O'B’.若点O'的横坐标为2,则点A'的坐标为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点A、B的坐标分别是(4,0)、(0,3),点O'在直线y=2x(x≥0)上,将△AOB沿射线OO'方向平移后得到△A'O'B’.若点O'的横坐标为2,则点A'的坐标为( )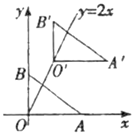 A、(4,4) B、(5,4) C、(6,4) D、(7,4)
A、(4,4) B、(5,4) C、(6,4) D、(7,4)二、填空题
-
9. 若 有意义,则 的取值范围为.10. 甲、乙二人在相同情况下,各射靶 次,两人命中环数的方差分别是 , ,则射击成绩较稳定的是.(填“甲”或“乙")11. 如图,菱形ABCD的周长是20,对角线AC、BD相交于点O.若BO=3,则菱形ABCD的面积为.
 12. 如图,在正方形ABCD中,E是边CD上的点.若△ABE的面积为4.5,DE=1,则BE的长为.
12. 如图,在正方形ABCD中,E是边CD上的点.若△ABE的面积为4.5,DE=1,则BE的长为.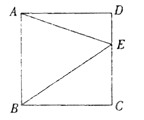 13. 如图,在▱ABCD中,E为边BC上一点,以AE为边作矩形AEFG.若∠BAE=40°,∠CEF=15°,则∠D的大小为度.
13. 如图,在▱ABCD中,E为边BC上一点,以AE为边作矩形AEFG.若∠BAE=40°,∠CEF=15°,则∠D的大小为度. 14. 如图,点A是函数 的图像上的一点,过点A作 轴,垂足为点B,点C为x轴上的一点,连接AC,BC,若△ABC的面积为4,则K的值为
14. 如图,点A是函数 的图像上的一点,过点A作 轴,垂足为点B,点C为x轴上的一点,连接AC,BC,若△ABC的面积为4,则K的值为
三、综合题
-
15. 计算:(1)、 .(2)、 .16. 如图,在矩形ABCD中,对角线AC、BD相交于点O.若∠AOD=120°,AB=3,求AC的长.
 17. 已知,在平面直角坐标系中,直线 经过点 和点 .(1)、求直线 所对应的函数表达式.(2)、若点 在直线 上,求 的值.18. (问题原型)如图,在 中,对角线 的垂直平分线 交 于点 ,交 于点 ,交 于点 .求证:四边形 是菱形.
17. 已知,在平面直角坐标系中,直线 经过点 和点 .(1)、求直线 所对应的函数表达式.(2)、若点 在直线 上,求 的值.18. (问题原型)如图,在 中,对角线 的垂直平分线 交 于点 ,交 于点 ,交 于点 .求证:四边形 是菱形.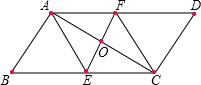
(小海的证法)证明:
是 的垂直平分线,
,(第一步)
,(第二步)
.(第三步)
四边形 是平行四边形.(第四步)
四边形 是菱形. (第五步)
(老师评析)小海利用对角线互相平分证明了四边形 是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
(挑错改错)
(1)、小海的证明过程在第步上开始出现了不正确.(2)、请你根据小海的证题思路写出此题的正确解答过程,19. 某校八年级甲,乙两班各有 名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取 名学生进行身体素质测试,测试成绩如下:甲班
乙班
整理上面数据,得到如下统计表:

样本数据的平均数、众数.中位数如下表所示:
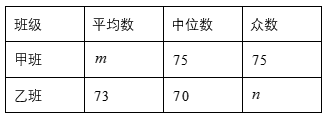
根据以上信息,解答下列问题:
(1)、求表中 的值(2)、表中 的值为(3)、若规定测试成绩在 分以上(含 分)的学生身体素质为优秀,请估计乙班 名学生中身体素质为优秀的学生的人数.20. 如图,在四边形ABCD中, ,E为边BC上一点,且EC=AD,连接AC.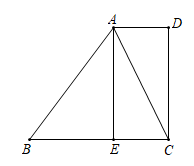 (1)、求证:四边形AECD是矩形;(2)、若AC平分∠DAB,AB=5,EC=2,求AE的长,21. 中国新版高铁“复兴号”率先在北京南站和上海虹桥站双向首发“复兴号”高铁从某车站出发,在行驶过程中速度 (千米/分钟)与时间 (分钟)的函数关系如图所示.
(1)、求证:四边形AECD是矩形;(2)、若AC平分∠DAB,AB=5,EC=2,求AE的长,21. 中国新版高铁“复兴号”率先在北京南站和上海虹桥站双向首发“复兴号”高铁从某车站出发,在行驶过程中速度 (千米/分钟)与时间 (分钟)的函数关系如图所示.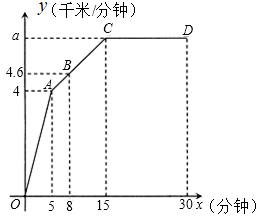 (1)、当 时,求 关于 工的函数表达式,(2)、求点 的坐标.(3)、求高铁在 时间段行驶的路程.22. 如图
(1)、当 时,求 关于 工的函数表达式,(2)、求点 的坐标.(3)、求高铁在 时间段行驶的路程.22. 如图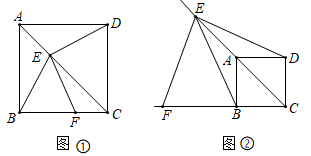
感知:如图①,在正方形ABCD中,点E在对角线AC上(不与点A、C重合),连结ED,EB,过点E作EF⊥ED,交边BC于点F.易知∠EFC+∠EDC=180°,进而证出EB=EF.
(1)、探究:如图②,点E在射线CA上(不与点A、C重合),连结ED、EB,过点E作EF⊥ED,交CB的延长线于点F.求证:EB=EF(2)、应用:如图②,若DE=2,CD=1,则四边形EFCD的面积为23. 如图,在平面直角坐标系中,函数 的图象经过点A(1,4)和点B.过点A作AC⊥x轴,垂足为点C,过点B作BD⊥y轴,垂足为点D,连结AB、BC、DC、DA.点B的横坐标为a(a>1)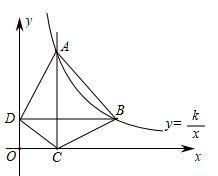 (1)、求k的值(2)、若△ABD的面积为4;
(1)、求k的值(2)、若△ABD的面积为4;①求点B的坐标,
②在平面内存在点E,使得以点A、B、C、E为顶点的四边形是平行四边形,直接写出符合条件的所有点E的坐标.
24. 如图,在平面直角坐标系中,点A的坐标为(0,6),点B在x轴的正半轴上.若点P、Q在线段AB上,且PQ为某个一边与x轴平行的矩形的对角线,则称这个矩形为点P、Q的“涵矩形”。下图为点P、Q的“涵矩形”的示意图.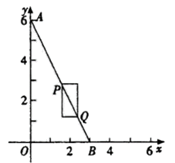 (1)、点B的坐标为(3,0);
(1)、点B的坐标为(3,0);①若点P的横坐标为 ,点Q与点B重合,则点P、Q的“涵矩形”的周长为.
②若点P、Q的“涵矩形”的周长为6,点P的坐标为(1,4),则点E(2,1),F(1,2),G(4,0)中,能够成为点P、Q的“涵矩形”的顶点的是.
(2)、四边形PMQN是点P、Q的“涵矩形”,点M在△AOB的内部,且它是正方形;①当正方形PMQN的周长为8,点P的横坐标为3时,求点Q的坐标.
②当正方形PMQN的对角线长度为/2时,连结OM.直接写出线段OM的取值范围.