吉林省长春市农安县2018-2019学年八年级下学期期末考试试卷

试卷更新日期：2020-05-18 类型：期末考试

进入出卷网下载

一、选择题

1. 无论 $x$ 取什么数，总有意义的分式是（）

A、 $\frac{5 x}{x^{4} + 3}$ B、 $\frac{2 x}{7 x + 8}$ C、 $\frac{x}{x^{3} + 2}$ D、 $\frac{x - 5}{x^{2}}$

查看试题解析
2. 若(x﹣2)^x＝1，则x的值是（）

A、0 B、1 C、3 D、0或3

查看试题解析
3. 如图所示，一次函数 $y = m x + m$ 的图像可能是（）

A、 B、 C、 D、

查看试题解析
4. 为了调查某种小麦的长势，从中抽取了10株麦苗，测得苗高（单位： $cm$ ）为16，9，14，11，12，10，16，8，17，19，则这组数据的中位数和众数分别是（）

A、11，11 B、12，11 C、13，11 D、13，16

查看试题解析
5. 无论a取何值，关于x的函数y＝﹣x+a²+1的图象都不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图，直线 $y = k x + b$ 交坐标轴于 $A (- 3 ， 0)$ 、 $B (0 ， 1)$ 两点，则不等式 $- k x - b < 0$ 的解集为（）

A、 $x < - 3$ B、 $x > - 3$ C、 $x < 3$ D、 $x > 3$

查看试题解析
7. 如图，平行四边形ABCD的对角线AC、BD相交于点O，下列结论正确的是（　　）

A、S_▱_ABCD=4S_△_AOB B、AC=BD C、AC⊥BD D、▱ABCD是轴对称图形

查看试题解析
8. 如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B为（）

A、66° B、104° C、114° D、124°

查看试题解析

二、填空题

9. 用科学记数法表示： $0.000002019 =$ ．

查看试题解析
10. 根据如图所示的程序，当输入x＝3时，输出的结果y＝.

查看试题解析
11. 若关于 $x$ 的方程 $\frac{3 x - 2}{x + 1} = 2 + \frac{m}{x + 1}$ 无解，则 $m$ 的值为．

查看试题解析
12. 现有甲、乙两支篮球队，每支球队队员身高的平均数均为1.85米，方差分别为 $S_{甲}^{2} = 0.32$ ， $S_{乙}^{2} = 0.36$ ，则身高较整齐的球队是队．

查看试题解析
13. 如图，▱ABCD与▱DCFE的周长相等，且∠BAD=60°，∠F=110°，则∠DAE的度数为°．

查看试题解析
14. 点A在双曲线y= $\frac{4}{x}$ 上，点B在双曲线y= $\frac{k}{x}$ （k≠0）上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是8，则k的值为．

查看试题解析

三、综合题

15. 解方程： $\frac{5 x - 4}{x - 2} = \frac{4 x + 10}{3 x - 6} - 1$ ．

查看试题解析
16. 以下是小明化简分式 $(\frac{x}{x^{2} + x} - 1) \div \frac{x^{2} - 1}{x^{2} + 2 x + 1}$ 的过程．
解：原式

$= (\frac{x}{x^{2} + x} - \frac{x^{2} + x}{x^{2} + x}) \div \frac{x^{2} - 1}{x^{2} + 2 x + 1}$                               ①

$= \frac{x - x^{2} + x}{x^{2} + x} \times \frac{x^{2} + 2 x + 1}{x^{2} - 1}$                                     ②

$= \frac{- x (x - 2) {(x + 1)}^{2}}{x {(x + 1)}^{2} (x - 1)}$                                           ③

$= \frac{2 - x}{x - 1}$                                                      ④

(1)、小明的解答过程在第步开始出错；

(2)、请你帮助小明写出正确的解答过程，并计算当 $x = 2$ 时分式的值．

查看试题解析
17. 甲、乙两个工程队合作完成一项工程，两队合做2天后由乙队单独做1天就完成了全部工程，已知乙队单独做所需的天数是甲队单独做所需天数的1.5倍，求甲、乙两队单独做各需多少天完成该项工程？

查看试题解析
18. 如图， $A E / / B F$ ， $B D$ 平分 $∠ A B C$ 交 $A E$ 于点 $D$ ， $A C ⊥ B D$ 于点 $O$ ，交 $B F$ 于点 $G$ ，连接 $C D$ ，求证：四边形 $A B C D$ 是菱形．

查看试题解析
19. 如图，点 A，B，C，D 依次在同一条直线上，点 E，F 分别在直线 AD 的两侧，已知 BE//CF，∠A=∠D，AE=DF.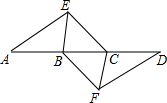

(1)、求证：四边形 BFCE 是平行四边形.

(2)、若 AD=10，EC=3，∠EBD=60°，当四边形 BFCE是菱形时，求 AB 的长.

查看试题解析
20. 如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A（ $- 3$ ， $\frac{3}{2}$ ），AB=1，AD=2．

(1)、直接写出B、C、D三点的坐标；

(2)、将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数 $y = \frac{k}{x}$ （ $x > 0$ ）的图象上，得矩形A′B′C′D′．求矩形ABCD的平移距离m和反比例函数的解析式．

查看试题解析

21. 我市某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.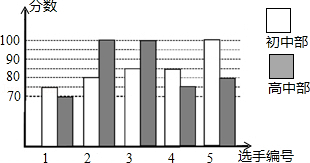

(1)、根据图示填写下表；

	平均数（分）	中位数（分）	众数（分）
初中部		85
高中部	85		100

(2)、结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；

(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.

查看试题解析

22. 如图，点E是正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．

(1)、求证：△ABF≌△CBE；

(2)、判断△CEF的形状，并说明理由．

查看试题解析
23. 某中学举行春季长跑比赛活动，小明从起点学校西门出发，途经市博物馆后按原路返还，沿比赛路线跑回终点学校西门．设小明离开起点的路程s（千米）与跑步时间t（分钟）之间的函数关系如图所示，其中从起点到市博物馆的平均速度是0.3千米/分钟，用时35分钟根据图象提供的信息，解答下列问题：

(1)、求图中 $a$ 的值，并求出 $O A$ 所在直线方程；

(2)、组委会在距离起点2.1千米处设立一个拍摄点 $C$ ，小明从第一次过点 $C$ 到第二次经过点 $C$ 所用的时间为68分钟
①求 $A B$ 所在直线的函数解析式；

②该运动员跑完赛程用时多少分钟？

查看试题解析
24. 定义：对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x⩾0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数。例如：一次函数y=x−1,它们的相关函数为y= ${\begin{cases} - x + 1 (x < 0) \\ x - 1 (x ⩾ 0) \end{cases}$ .

(1)、已知点A(−5,8)在一次函数y=ax−3的相关函数的图象上，求a的值；

(2)、已知二次函数y=−x $^{2}$ +4x− $\frac{1}{2}$ .
①当点B(m, $\frac{3}{2}$ )在这个函数的相关函数的图象上时，求m的值；

②当−3⩽x⩽3时,求函数y=−x $^{2}$ +4x− $\frac{1}{2}$ 的相关函数的最大值和最小值.

查看试题解析