吉林省长春市宽城区2018-2019学年八年级下学期期末考试试卷
试卷更新日期:2020-05-18 类型:期末考试
一、选择题
-
1. 要使二次根式 有意义,则x的取值范围是( )A、 . B、 . C、 . D、 .2. 在平面直角坐标系的第一象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是( )A、(3,-4). B、(4,-3). C、(3,4). D、(4,3).3. 为参加学校举办的“诗意校园•致远方”朗诵艺术大赛,八年级“屈原读书社”组织了五次选拔赛,这五次选拔赛中,小明五次成绩的平均数是90,方差是2;小强五次成绩的平均数也是90,方差是14.8.下列说法正确的是( )A、小明的成绩比小强稳定 B、小明、小强两人成绩一样稳定 C、小强的成绩比小明稳定 D、无法确定小明、小强的成绩谁更稳定4. 如图,在平面直角坐标系中,函数 和 的图象交于点P,则根据图象可得,关于x、y的二元一次方程组 的解是( )
 A、 . B、 . C、 . D、 .5. 如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于 ( )
A、 . B、 . C、 . D、 .5. 如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于 ( )
 A、1 B、 C、 D、6. 如图,在平面直角坐标系中,菱形ABCD的顶点A、B的坐标分别为(3,0)、(-2,0),点D在y轴正半轴上,则点C的坐标为( )
A、1 B、 C、 D、6. 如图,在平面直角坐标系中,菱形ABCD的顶点A、B的坐标分别为(3,0)、(-2,0),点D在y轴正半轴上,则点C的坐标为( ) A、(-3,4). B、(-4,3). C、(-5,3). D、(-5,4).7. 如图,在四边形ABCD中,E是BC的中点,连接DE并延长,交AB的延长线于点F , AB=BF , 添加一个条件,使四边形ABCD是平行四边形.下列条件中正确的是( )
A、(-3,4). B、(-4,3). C、(-5,3). D、(-5,4).7. 如图,在四边形ABCD中,E是BC的中点,连接DE并延长,交AB的延长线于点F , AB=BF , 添加一个条件,使四边形ABCD是平行四边形.下列条件中正确的是( ) A、AD=BC B、CD=BF C、∠F=∠CDE D、∠A=∠C8. 如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数 (k≠0,x>0)的图象上,点D的坐标为(﹣4,1),则k的值为( )
A、AD=BC B、CD=BF C、∠F=∠CDE D、∠A=∠C8. 如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数 (k≠0,x>0)的图象上,点D的坐标为(﹣4,1),则k的值为( )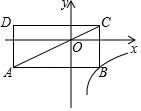 A、 B、 C、4 D、﹣4
A、 B、 C、4 D、﹣4二、填空题
-
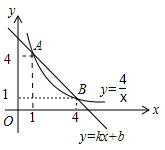
9. 与最简二次根式5 是同类二次根式,则a= .10. 某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95、90、88,则小彤这学期的体育成绩为分.11. 如图,在平面直角坐标系中,一次函数 和函数 的图象交于A、B两点.利用函数图象直接写出不等式 的解集是.
 12. 如图,在 中, , .对角线AC与BD相交于点O, ,则BD 的长为.
12. 如图,在 中, , .对角线AC与BD相交于点O, ,则BD 的长为. 13. 如图,矩形ABCD的对角线AC与BD相交于点O, , .若 , ,则四边形OCED的面积为.
13. 如图,矩形ABCD的对角线AC与BD相交于点O, , .若 , ,则四边形OCED的面积为. 14. 如图,在正方形ABCD中,等边三角形AEF的顶点E,F分别在边BC和CD上,则∠AEB=.
14. 如图,在正方形ABCD中,等边三角形AEF的顶点E,F分别在边BC和CD上,则∠AEB=.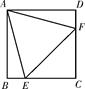
三、综合题
-
15. 计算:( + )×16. 图①,图②均是 的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A在格点上.试在网格中画出顶点在格点上,面积为6,且符合相应条件的图形.
 (1)、在图①中,画出以点A为顶点的非特殊的平行四边形.(2)、在图②中,画出以点A为对角线交点的非特殊的平行四边形.17. 如图,在平面直角坐标系中,正比例函数 与函数 的图象相交于点 , 轴于点B.平移直线 ,使其经过点B,得到直线l,求直线l所对应的函数表达式.
(1)、在图①中,画出以点A为顶点的非特殊的平行四边形.(2)、在图②中,画出以点A为对角线交点的非特殊的平行四边形.17. 如图,在平面直角坐标系中,正比例函数 与函数 的图象相交于点 , 轴于点B.平移直线 ,使其经过点B,得到直线l,求直线l所对应的函数表达式. 18. 如图,已知四边形ABCD是平行四边形,点E , F分别是AB , BC上的点,AE=CF , 并且∠AED=∠CFD.
18. 如图,已知四边形ABCD是平行四边形,点E , F分别是AB , BC上的点,AE=CF , 并且∠AED=∠CFD.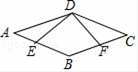
求证:
(1)、△AED≌△CFD;(2)、四边形ABCD是菱形.19. 如图,在四边形AECF中, .CE、CF分别是△ABC的内,外角平分线. (1)、求证:四边形AECF是矩形.(2)、当△ABC满足什么条件时,四边形AECF是正方形?请说明理由.20. 某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级学生参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取10名学生的成绩,数据如下(单位:分):
(1)、求证:四边形AECF是矩形.(2)、当△ABC满足什么条件时,四边形AECF是正方形?请说明理由.20. 某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级学生参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取10名学生的成绩,数据如下(单位:分):七年级 88 94 90 94 84 94 99 94 99 100
八年级 84 93 88 94 93 98 93 98 97 99
整理数据:按如下分数段整理数据并补全表格:
成绩x
人数 年级
七年级
1
1
5
3
八年级
4
4
分析数据:补全下列表格中的统计量:
统计量
年级
平均数
中位数
众数
方差
七年级
93.6
94
24.2
八年级
93.7
93
20.4
得出结论:你认为哪个年级学生“汉字听写”大赛的成绩比较好?并说明理由.(至少从两个不同的角度说明推断的合理性)
21. 某种水泥储存罐的容量为25立方米,它有一个输入口和一个输出口.从某时刻开始,只打开输入口,匀速向储存罐内注入水泥,3分钟后,再打开输出口,匀速向运输车输出水泥,又经过2.5分钟储存罐注满,关闭输入口,保持原来的输出速度继续向运输车输出水泥,当输出的水泥总量达到8立方米时,关闭输出口.储存罐内的水泥量y(立方米)与时间x(分)之间的部分函数图象如图所示.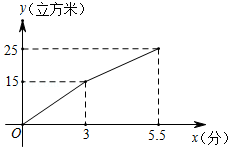 (1)、求每分钟向储存罐内注入的水泥量.
(1)、求每分钟向储存罐内注入的水泥量.
(2)、当3≤x≤5.5时,求y与x之间的函数关系式.(3)、储存罐每分钟向运输车输出的水泥量是立方米,从打开输入口到关闭输出口共用的时间为分钟.
22. 已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断:①OA=OC,②AB=CD,③∠BAD=∠DCB,④AD∥BC.
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)、构造一个真命题,画图并给出证明;(2)、构造一个假命题,举反例加以说明.23. 如图,在矩形ABCD中, , .将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.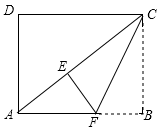 (1)、求线段AC的长.(2)、求线段EF的长.(3)、点G在线段CF上,在边CD上存在点H,使以E、F、G、H为顶点的四边形是平行四边形,请画出 ,并直接写出线段DH的长.24. 如图,四边形ABCD的四个顶点分别在反比例函数 与 (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)、求线段AC的长.(2)、求线段EF的长.(3)、点G在线段CF上,在边CD上存在点H,使以E、F、G、H为顶点的四边形是平行四边形,请画出 ,并直接写出线段DH的长.24. 如图,四边形ABCD的四个顶点分别在反比例函数 与 (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4. (1)、当m=4,n=20时.
(1)、当m=4,n=20时.①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)、四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.