广西北海市2018-2019学年高一下学期数学期中考试试卷

试卷更新日期：2020-05-18 类型：期中考试

进入出卷网下载

一、单选题

1. 将参加夏令营的400名学生编号为：001，002，…，400，采用系统抽样的方法抽取一个容量为40的样本，且随机抽得的号码为003，这400名学生分住在三个营区，从001到180在第一营区，从181到295在第二营区，从296到400在第三营区，三个营区被抽中的人数分别为（）

A、18，12，10 B、20，12，8 C、17，13，10 D、18，11，11

查看试题解析
2. 某中学共有1000名学生，其中高一年级350人，该校为了了解本校学生视力情况，用分层抽样的方法从该校学生中抽出一个容量为100的样本进行调查，则应从高一年级抽取的人数为（）

A、20 B、25 C、30 D、35

查看试题解析
3. 某学校为落实学生掌握社会主义核心价值观的情况，用系统抽样的方法从全校2400名学生中抽取30人进行调查.现将2400名学生随机地从1～2400编号，按编号顺序平均分成30组（1～80号，81～160号，…，2321～2400号），若第3组与第4组抽出的号码之和为432，则第6组抽到的号码是（）

A、416 B、432 C、448 D、464

查看试题解析
4. 军训时，甲、乙两名同学进行射击比赛，共比赛10场，每场比赛各射击四次，且用每场击中环数之和作为该场比赛的成绩．数学老师将甲、乙两名同学的10场比赛成绩绘成如图所示的茎叶图，并给出下列4个结论：(1)甲的平均成绩比乙的平均成绩高；(2)甲的成绩的极差是29；(3)乙的成绩的众数是21；(4)乙的成绩的中位数是18．则这4个结论中，正确结论的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 甲乙两名同学 $6$ 次考试的成绩统计如图，甲乙两组数据的平均数分别为 $\bar{x_{甲}}$ ， $\bar{x_{乙}}$ ，方差分别为 $σ_{甲}^{2}$ ， $σ_{乙}^{2}$ ，则（）

A、 $\bar{x_{甲}} > \bar{x_{乙}}$ ， $σ_{甲}^{2} < σ_{乙}^{2}$ B、 $\bar{x_{甲}} > \bar{x_{乙}}$ ， $σ_{甲}^{2} > σ_{乙}^{2}$ C、 $\bar{x_{甲}} < \bar{x_{乙}}$ ， $σ_{甲}^{2} < σ_{乙}^{2}$ D、 $x_{甲} < x_{乙}$ ， $σ_{甲}^{2} > σ_{乙}^{2}$

查看试题解析
6. 今有一组实验数据如下：

$x$

$1.99$

$3.0$

$4.0$

$5.1$

$6.12$

$y$

$1.5$

$4.04$

$7.5$

$12$

$18.01$

分别用下列函数模型来拟合变量 $y$ 与 $x$ 之间的关系，其中拟合效果最好的是（）

A、 $y = \frac{1}{2} (x^{2} - 1)$ B、 $y = \log_{\frac{1}{2}} x$ C、 $y = \log_{2} x$ D、 $y = 2 x - 2$

查看试题解析
7. 某程序框图如图所示，若输出的S=26，则判断框内应填( )

A、k>3? B、k>4? C、k>5? D、k>6?

查看试题解析
8. 按照程序框图（如图）执行，第4个输出的数是（）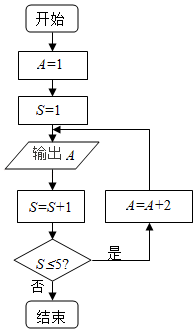

A、5 B、6 C、7 D、8

查看试题解析
9. 按下面的流程图进行计算.若输出的 $x = 202$ ，则输入的正实数x值的个数最多为（）

A、 $2$ B、 $3$ C、 $4$ D、 $5$

查看试题解析
10. 已知随机事件 $A$ 和 $B$ 互斥，且 $P (A \cup B) = 0.7$ ， $P (B) = 0.2$ ，则 $P (\bar{A}) =$ （）

A、0.5 B、0.1 C、0.7 D、0.8

查看试题解析
11. 小明需要从甲城市编号为1-14的14个工厂或乙城市编号为15-32的18个工厂中选择一个去实习，设“小明在甲城市实习”为事件A，“小明在乙城市且编号为3的倍数的工厂实习”为事件B，则P(A+B)=（）

A、 $\frac{3}{32}$ B、 $\frac{5}{8}$ C、 $\frac{9}{16}$ D、 $\frac{1}{4}$

查看试题解析
12. 如图，半径为1的圆内有一阴影区域，在圆内随机撒入一大把豆子，共 $n$ 颗，其中，落在阴影区域内的豆子共 $m$ 颗，则阴影区域的面积约为（）

A、 $\frac{m}{n}$ B、 $\frac{n}{m}$ C、 $\frac{m π}{n}$ D、 $\frac{n π}{m}$

查看试题解析

二、填空题

13. 交通部门对某路段公路上行驶的汽车速度实施监控，从速度不小于 $50 k m / h$ 的汽车中抽取200辆汽车进行测速分析，得到如图所示的时速的频率分布直方图，则时速在 $80 k m / h$ 以上的汽车有辆.

查看试题解析
14. 若某中学高二年级8个班参加合唱比赛的得分如茎叶图所示，则这组数据的中位数是．

查看试题解析
15. 某兴趣小组有2名男生和3名女生，现从中任选2名学生去参加活动，则恰好选中1名女生1名男生的概率为．

查看试题解析
16. 在一次教师联欢会上，到会的女教师比男教师多12人，从这些教师中随机挑选一人表演节目，若选到男教师的概率为 $\frac{9}{20}$ ，则参加联欢会的教师人数为．

查看试题解析

三、解答题

17. 随着“互联网＋交通”模式的迅猛发展，“共享助力单车”在很多城市相继出现．某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度，随机调查了100名用户，得到用户的满意度评分，现将评分分为5组，如下表：

组别	一	二	三	四	五
满意度评分	[0，2）	[2，4）	[4，6）	[6，8）	[8，10]
频数	5	10	a	32	16
频率	0.05	b	0.37	c	0.16

(1)、求表格中的a，b，c的值；

(2)、估计用户的满意度评分的平均数；

(3)、若从这100名用户中随机抽取25人，估计满意度评分低于6分的人数为多少？

查看试题解析

18. 某校举行书法比赛，下图为甲乙两人近期 $8$ 次参加比赛的成绩的茎叶图。如图所示，甲的成绩中有一个数的个位数字模糊，在茎叶图中用 $a$ 表示。

(1)、假设 $a = 4$ ，求甲的成绩的平均数；

(2)、假设数字 $a$ 的取值是随机的，求乙的平均数高于甲的概率。

查看试题解析
19. 在如图所示的程序框图中，有这样一个执行框 $x_{i} = f (x_{i - 1})$ ，其中的函数关系式为 $f (x) = \frac{4 x - 2}{x + 1}$ ，程序框图中的 $D$ 为函数 $f (x)$ 的定义域．

(1)、若输入 $x_{0} = \frac{49}{65}$ ，请写出输出的所有 $x$ 的值；

(2)、若输出的所有 $x_{i}$ 都相等，试求输入的初始值 $x_{0}$ ．

查看试题解析
20. 某老师是省级课题组的成员，主要研究课堂教学目标达成度，为方便研究，从实验班中随机抽取30次的随堂测试成绩进行数据分析.已知学生甲的30次随堂测试成绩如下（满分为100分）：

(1)、把学生甲的成绩按 $[30 ， 40)$ ， $[40 ， 50)$ ， $[50 ， 60)$ ， $[60 ， 70)$ ， $[70 ， 80)$ ， $[80 ， 90]$ 分成6组，列出频率分布表，并画出频率分布直方图：

(2)、为更好的分析学生甲存在的问题，从随堂测试成绩50分以下（不包括50分）的试卷中随机抽取3份进行分析，求恰有2份成绩在 $[30 ， 40)$ 内的概率.

查看试题解析
21. 某港口船舶停靠的方案是先到先停.

(1)、若甲乙两艘船同时到达港口，双方约定各派一名代表猜拳：从 $1, 2, 3, 4, 5$ 中各随机选一个数，若两数之和为奇数，则甲先停靠；若两数之和为偶数，则乙先停靠，这种对着是否公平？请说明理由.

(2)、根据已往经验，甲船将于早上 $7 : 00 - 8 : 00$ 到达，乙船将于早上 $7 : 30 - 8 : 30$ 到达，请应用随机模拟的方法求甲船先停靠的概率，随机数模拟实验数据参考如下：记 $X, Y$ 都是 $0 \sim 1$ 之间的均匀随机数，用计算机做了 $100$ 次试验，得到的结果有 $12$ 次满足 $X - Y \geq 0.5$ ，有 $6$ 次满足 $X - 2 Y \geq 0.5$ .

查看试题解析
22. 一台还可以用的机器由于使用的时间较长，它按不同的转速生产出来的某机械零件有一些会有缺陷，每小时生产有缺陷零件的多少随机器运转的速率而变化，下表为抽样试验结果：

转速x（转/秒）

16

14

12

8

每小时生产有缺陷的零件数y（件）

11

9

8

5

(1)、画出散点图；

(2)、如果y与x有线性相关的关系，求回归直线方程；

(3)、若实际生产中，允许每小时生产的产品中有缺陷的零件最多为10个，那么机器的运转速度应控制在什么范围内？

查看试题解析

$x$	$1.99$	$3.0$	$4.0$	$5.1$	$6.12$
$y$	$1.5$	$4.04$	$7.5$	$12$	$18.01$

转速x（转/秒）	16	14	12	8
每小时生产有缺陷的零件数y（件）	11	9	8	5