吉林省长春市朝阳区2018-2019学年八年级下学期期末考试试卷

试卷更新日期：2020-05-18 类型：期末考试

进入出卷网下载

一、选择题

1. 函数 $y = \frac{6}{x - 3}$ 的自变量 $x$ 的取值范围是（）

A、 $x \neq 3$ B、 $x > 3$ C、 $x < 3$ D、 $x = 3$

查看试题解析
2. 芝麻的用途广泛，经测算，一粒芝麻约有0. 00000201千克. 数据0. 00000201用科学记数法表示为（）

A、 $0.20 \times 10^{- 5}$ B、 $2.01 \times 10^{- 5}$ C、 $2.01 \times 10^{- 6}$ D、 $20.1 \times 10^{- 7}$

查看试题解析
3. 若反比例函数 $y = \frac{k}{x}$ 的图象经过点 $(- 1 ， - 2)$ ，则该反比例函数的图象位于（）

A、第一、二象限 B、第二、三象限 C、第二、四象限 D、第一、三象限

查看试题解析
4. 若一次函数 $y = 2 x - 1$ 向上平移2个单位，则平移后得到的一次函数的图象与 $y$ 轴的交点为（）

A、 $(0, - 1)$ B、 $(0, - 3)$ C、 $(0, 1)$ D、 $(0, 2)$

查看试题解析
5. 在一次“爱心互助”捐款活动中，某班第一小组7名同学捐款的金额(单位：元)分别为6，3，6，5，5，6，9.这组数据的中位数和众数分别是（）

A、5，5 B、6，6 C、6，5 D、5，6

查看试题解析
6. 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（　　）

A、①，② B、①，④ C、③，④ D、②，③

查看试题解析
7. 如图， O 为矩形 ABCD 的对角线 AC 的中点，过点 O 作 AC 的垂线 EF 分别交 AD 、 BC 于点 E 、 F ，连结 CE .若该矩形的周长为20，则 $△ C D E$ 的周长为（）

A、10 B、9 C、8 D、5

查看试题解析
8. 如图，在平面直角坐标系中，点 $A (3 ， 2)$ 在反比例函数 $y = \frac{k}{x}$ 的图象上.若 $y < 2$ ，则自变量 $x$ 的取值范围是（）

A、 $x < 3$ B、 $x > 3$ C、 $x > 3$ 且 $x \neq 0$ D、 $x > 3$ 或 $x < 0$

查看试题解析

二、填空题

9. 计算： ${(π + 2)}^{0} =$ .

查看试题解析
10. 一组数据为5，7，3， $x$ ，6，4. 若这组数据的众数是5，则该组数据的平均数是.

查看试题解析
11. 如图，在正方形 $A B C D$ 中，点 $P$ 、 $Q$ 在对角线 $B D$ 上，分别过点 $P$ 、 $Q$ 作边 $C D$ 的平行线交 $B C$ 于点 $E$ 、 $H$ ，作边 $A D$ 的平行线交 $A B$ 于点 $F$ 、 $G$ . 若 $A B = 2$ ，则图中阴影部分图形的面积和为.

查看试题解析
12. 在平面直角坐标系中，一次函数 $y = k x + b$ ( $k$ 、 $b$ 为常数， $k \neq 0$ )的图象如图所示，根据图象中的信息可求得关于 $x$ 的方程 $k x + b = 3$ 的解为.

查看试题解析
13. 如图， $E$ 是菱形 $A B C D$ 的对角线 $B D$ 上一点，过点 $E$ 作 $E F ⊥ B C$ 于点 $F$ . 若 $E F = 4$ ，则点 $E$ 到边 $A B$ 的距离为.

查看试题解析
14. 如图，在 $▱ A B C D$ 中， $E$ 为边 $B C$ 延长线上一点，且 $C E = 2 B C$ ，连结 $A E$ 、 $D E$ .若 $△ A D E$ 的面积为1，则 $△ A B E$ 的面积为.

查看试题解析

三、综合题

15. 先化简，再求值： $(1 - \frac{1}{a - 2}) \div \frac{a - 3}{a^{2} - 4 a + 4}$ ，其中 $a = 2019$ .

查看试题解析
16. 如图，四边形 $A B C D$ 和 $B E F C$ 都是平行四边形.求证：四边形 $A E F D$ 是平行四边形.

查看试题解析

17. 已知

y

是

x

的函数，自变量

x

的取值范围为

x \geq 0

，下表是

y

与

x

的几组对应值

$x$	0	1	2	3	3.5	4	4.5	…
$y$	1	2	3	4	3	2	1	…

小明根据学习函数的经验，利用上述表格所反映出的 $y$ 与 $x$ 之间的变化规律，对该函数的图象与性质进行了探究.下面是小明的探究过程，请补充完整：

(1)、如图，在平面直角坐标系中，指出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象.

(2)、根据画出的函数图象填空.

该函数图象与 $x$ 轴的交点坐标为.

(3)、直接写出该函数的一条性质.

查看试题解析

18. 市政某小组检修一条长 $1200 m$ 的自来水管道，在检修了一半的长度后，提高了工作效率，每小时检修的管道长度是原计划的1.5倍，结果共用 $5 h$ 完成任务，求这个小组原计划每小时检修管道的长度.

查看试题解析
19. 如图，正方形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $C E / / B D$ ， $D E / / A C$ .

(1)、求证：四边形 $O C E D$ 是正方形.

(2)、若 $A C = \sqrt{2}$ ，则点 $E$ 到边 $A B$ 的距离为.

查看试题解析

20. 要从甲、乙两名同学中选出一名，代表班级参加射击比赛. 现将甲、乙两名同学参加射击训练的成绩绘制成下列两个统计图：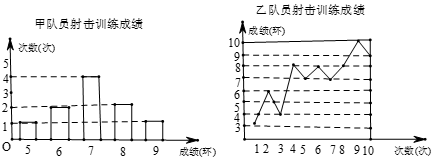

根据以上信息，整理分析数据如下：

	平均成绩(环)	中位数(环)	众数(环)	方差( $环^{2}$ )
甲	7	$b$	7	1. 2
乙	$a$	7. 5	$c$	4. 2

(1)、分别求表格中

a

、

b

、

c

的值.

(2)、如果其他参赛选手的射击成绩都在7环左右，应该选队员参赛更适合；如果其他参赛选手的射击成绩都在8环左右，应该选队员参赛更适合.

查看试题解析

21. 如图，在平面直角坐标系中，菱形 $A B C D$ 的顶点 $C$ 与原点 $O$ 重合，点 $B$ 在 $y$ 轴的正半轴上，点 $A$ 在函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上，点 $D$ 的坐标为 $(4 ， 3)$ .

(1)、求 $k$ 的值.

(2)、将点 $D$ 沿 $x$ 轴正方向平移得到点 $D^{'}$ ，当点 $D^{'}$ 在函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上时，求 $D D^{'}$ 的长.

查看试题解析
22. 图①、图②、图③都是由8个大小完全相同的矩形拼成无重叠、无缝隙的图形，每个小矩形的顶点叫做格点，线段 $A B$ 的端点都在格点上. 仅用无刻度的直尺分别在下列方框内完成作图，保留作图痕迹.

(1)、在图①中，作线段 $A B$ 的一条垂线 $M N$ ，点 $M$ 、 $N$ 在格点上.

(2)、在图②、图③中，以 $A B$ 为边，另外两个顶点在格点上，各画一个平行四边形，所画的两个平行四边形不完全重合.

查看试题解析
23. 五一期间，甲、乙两人分别骑自行车和摩托车从 $A$ 地出发前往 $B$ 地郊游，并以各自的速度匀速行驶，到达目的地停止，途中乙休息了一段时间，然后又继续赶路.甲、乙两人各自行驶的路程 $y (k m)$ 与所用时间 $x (\min)$ 之间的函数图象如图所示.

(1)、甲骑自行车的速度是 $k m / \min$ .

(2)、求乙休息后所行的路程 $y$ 与 $x$ 之间的函数关系式，并写出自变量 $x$ 的取值范围.

(3)、为了保证及时联络，甲、乙两人在第一次相遇时约定此后两人之间的路程不超过 $3 k m$ .甲、乙两人是否符合约定，并说明理由.

查看试题解析
24. 如图

(1)、（问题情境）在综合实践课上，同学们以“图形的平移”为主题开展数学活动，如图①，先将一张长为4，宽为3的矩形纸片沿对角线剪开，拼成如图所示的四边形 $A B C D$ ， $A D = 3$ ， $B D = 4$ ，则拼得的四边形 $A B C D$ 的周长是.

(2)、（操作发现）将图①中的 $△ A B E$ 沿着射线 $D B$ 方向平移，连结 $A D$ 、 $B C$ 、 $A F$ 、 $C E$ ，如图②.当 $△ A B E$ 的平移距离是 $\frac{1}{2} B E$ 的长度时，求四边形 $A E C F$ 的周长.

(3)、（操作探究）将图②中的 $△ A B E$ 继续沿着射线 $D B$ 方向平移，其它条件不变，当四边形 $A B C D$ 是菱形时，将四边形 $A B C D$ 沿对角线剪开，用得到的四个三角形拼成与其面积相等的矩形，直接写出所有可能拼成的矩形周长.

查看试题解析