吉林省伊通满族自治县2018-2019学年八年级下学期期末考试试卷

试卷更新日期：2020-05-18 类型：期末考试

进入出卷网下载

一、选择题

1. 函数y= $\sqrt{x - 2}$ 的自变量的取值范围是（）

A、x≥2 B、x＜2 C、x＞2 D、x≤2

查看试题解析
2. 下列四组线段中，可以构成直角三角形的是（）

A、3,4,5 B、 $1, \sqrt{2}, 3$ C、4,5,6 D、1,1,2

查看试题解析
3. 如图，在▱ABCD中，下列结论不一定正确的是（）

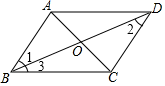A、∠1＝∠2 B、∠1＝∠3 C、AB＝CD D、∠BAD＝∠BCD

查看试题解析
4. 在四边形 $A B C D$ 中， $∠ A = ∠ B = ∠ C = 90 °$ ，如果再添加一个条件，即可推出该四边形是正方形，这个条件可以是（）

A、 $B C = C D$ B、 $A B = C D$ C、 $∠ D = 90 °$ D、 $A D = B C$

查看试题解析
5. 已知甲、乙、丙三个旅行团的游客人数都相等，且每个旅行团游客的平均年龄都是35岁，这三个旅行团游客年龄的方差分别是 $s_{甲}^{2} = 17$ ， $s_{乙}^{2} = 14.6$ ， $s_{丙}^{2} = 19$ ，如果你最喜欢带游客年龄相近的旅行团，若在三个旅行团中选一个，则你应选择（）

A、甲团 B、乙团 C、丙团 D、采取抽签方式，随便选一个

查看试题解析
6. 如图，已知正比例函数 $y_{1} = a x$ 与一次函数 $y_{2} = - \frac{1}{2} x + b$ 的图象交于点 $P$ .下面四个结论中正确的是（）

A、 $a > 0$ B、 $b < 0$ C、当 $x < 0$ 时， $y_{1} > y_{2}$ D、当 $x > 2$ 时， $y_{1} < y_{2}$

查看试题解析

二、填空题

7. 计算：( $- \sqrt{5}$ )²=。

查看试题解析
8. 已知有两点 $A (1, y_{1})$ 、 $B (- 2, y_{2})$ 都在一次函数 $y = - 3 x + n$ 的图象上，则 $y_{1}, y_{2}$ 的大小关系是（用“<”连接）

查看试题解析
9. 已知一组数据3、a、4、6的平均数为4，则这组数据的中位数是.

查看试题解析
10. 如图，公路 $A C ， B C$ 互相垂直，公路 $A B$ 的中点 $M$ 与点 $C$ 被湖隔开，若测得 $A B$ 的长为2.4km，则 $M ， C$ 两点间的距离为km.

查看试题解析
11. 如图，四边形 $A B C D$ 是正方形，延长 $A B$ 到点 $E$ ，使 $A E = A C$ ，则 $∠ B C E$ 的度数是。

查看试题解析
12. 菱形的两条对角线的长分别为6和8，则这个菱形的周长为.

查看试题解析
13. 如图，在平面直角坐标系中，矩形OABC的顶点A在y轴正半轴上，边AB、OA(AB>OA)的长分别是方程x $^{2}$ −11x+24=0的两个根，D是AB上的一动点(不与A．B重合).AB=8，OA=3.若动点D满足△BOC与AOD相似，则直线OD的解析式为.

查看试题解析
14. 小明用四根长度相同的木条制作了能够活动的菱形学具，他先把活动学具成为图1所示菱形，并测得 $∠ B = 60 °$ ，接着活动学具成为图2所示正方形，并测得正方形的对角线 $A C = \sqrt{2} a$ cm，则图1中对角线 $A C$ 的长为cm.

查看试题解析

三、综合题

15. 计算： $\sqrt{27} \times \sqrt{\frac{1}{3}} - (\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})$ .

查看试题解析
16. 如图所示，在▱ABCD中，E，F是对角线BD上的两点，且BE=DF，求证：AE=CF

查看试题解析
17. 《九章算术》卷九“勾股”中记载：今有池方一丈，葭生其中央，出水一尺.引葭赴岸，适与岸齐.问霞长几何.
注释：今有正方形水池边长1丈，芦苇生长在中央，长出水面1尺.将芦苇向池岸牵引，恰好与水岸齐，问芦苇的长度（一丈等于10尺）.解决下列问题：

(1)、示意图中，线段 $A F$ 的长为尺，线段 $E F$ 的长为尺；

(2)、求芦苇的长度.

查看试题解析
18. 小红帮弟弟荡秋千(如图1)，秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示．

(1)、根据函数的定义，请判断变量h是否为关于t的函数?

(2)、结合图象回答：
①当t=0.7s时，h的值是多少?并说明它的实际意义．

②秋千摆动第一个来回需多少时间?

查看试题解析
19. 如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，在现有网格中，以格点为顶点，分别按下列要求画三角形。

(1)、在图1中，画一个等腰直角三角形，使它的面积为5；

(2)、在图2中，画一个三角形，使它的三边长分别为3，2 $\sqrt{2}$ ， $\sqrt{5}$ ；

(3)、在图3中，画一个三角形，使它的三边长都是有理数.

查看试题解析
20. 如图，在平面直角坐标系xOy中，直线 $l$ 的表达式为 $y = 2 x - 6$ ，点A ， B的坐标分别为（1，0），（0，2），直线AB与直线 $l$ 相交于点P ．

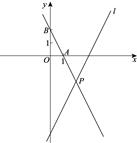(1)、求直线AB的表达式；

(2)、求点P的坐标；

(3)、若直线 $l$ 上存在一点C ，使得△APC的面积是△APO的面积的2倍，直接写出点C的坐标．

查看试题解析

21. 《中国诗词大会》是央视首档全民参与的诗词节目，节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨，其中的一个比赛环节“飞花令”增加了节目悬念.新学期开学，某班组织了甲、乙两组同学进行了“飞花令”的对抗赛，规定说对一首得1分，比赛中有一方说出9首就结束两个人对抗，得6分以上为合格，得9分以上为优秀，甲、乙两组同学的一次测试成绩如下：

甲组：9，4，6，5，9，6，7，6，8，6，9，5，7，6，9

乙组：4，6，7，6，7，9，7，5，8，7，6，7，9，6，8

(1)、请你根据所给的两组数据，绘制统计图（表）.

(2)、把下面的表格补充完整.

统计量	平均分（分）	方差（分²）	中位数（分）	合格率	优秀率
甲组		2.56	6	80.0%	26.7%
乙组	6.8	1.76		86.7%	13.3%

(3)、根据第（2）题表中数据，你会支持哪一组，并说明理由.

查看试题解析

22. 如图，在矩形ABCD中，对角线AC的垂直平分线EF分别交AD，AC，BC于点E，O，F，连接CE和AF．

(1)、求证：四边形AECF为菱形；

(2)、若AB=4，BC=8，求菱形AECF的周长．

查看试题解析
23. 我们给出如下定义：把对角线互相垂直的四边形叫做“正交四边形”.
如图1，在四边形 $A B C D$ 中， $A C ⊥ B D$ ，四边形 $A B C D$ 就是“正交四边形”.

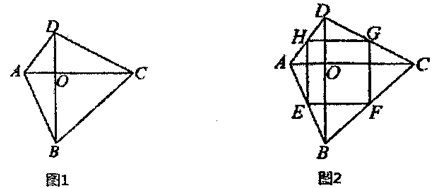(1)、下列四边形，一定是“正交四边形”的是.
①平行四边形②矩形③菱形④正方形

(2)、如图2，在“正交四边形” $A B C D$ 中，点 $E 、 F 、 G 、 H$ 分别是边 $A B 、 B C 、 C D 、 D A$ 的中点，求证：四边形 $E F G H$ 是矩形.

(3)、小明说：“计算‘正交四边形’的面积可以仿照菱形的方法，面积是对角线之积的一半.”小明的说法正确吗？如果正确，请给出证明；如果不正确，请给出反例.

查看试题解析
24. 甲乙两车分别从A．B两地相向而行，甲车出发1小时后乙车出发，并以各自速度匀速行驶，两车相遇后依然按照原速度原方向各自行驶，如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象，其中D点表示甲车到达B地，停止行驶。

(1)、A、B两地的距离千米；乙车速度是；a=.

(2)、乙出发多长时间后两车相距330千米?

查看试题解析