吉林省松原市前郭县2018-2019学年八年级下学期期末考试试卷

试卷更新日期：2020-05-18 类型：期末考试

进入出卷网下载

一、选择题

1. 要使 $\sqrt{2 x + 5}$ 有意义， $x$ 必须满足（）

A、 $x \geq - \frac{5}{2}$ B、 $x \leq - \frac{5}{2}$ C、 $x$ 为任何实数 D、 $x$ 为非负数

查看试题解析
2. 下列二次根式① $\sqrt{12}$ ，② $\sqrt{2^{2}}$ ，③ $\sqrt{\frac{2}{3}}$ ，④ $\sqrt{27}$ ，能与 $\sqrt{3}$ 合并的是（）

A、①和② B、②和③ C、①和④ D、③和④

查看试题解析
3. 如果p(2，m)，A（1，1）,B（4，0）三点在同一条直线，那么m的值为（）

A、2 B、- $\frac{2}{3}$ C、 $\frac{2}{3}$ D、1

查看试题解析
4. 已知AC为矩形ABCD的对角线，则图中∠1与∠2一定不相等的是（　　）

A、 B、 C、 D、

查看试题解析
5. 如图，点 E ， F 是▱ABCD 对角线上两点，在条件①DE＝BF；②∠ADE＝∠CBF； ③AF＝CE；④∠AEB＝∠CFD 中，添加一个条件，使四边形 DEBF 是平行四边形，可添加的条件是（）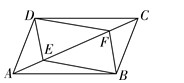

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
6. 如图，2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》（也称《赵爽弦图》），它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，如果大正方形的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长直角边为b，那么 $（ a + b ）^{2}$ 的值为（）

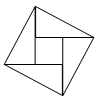A、13 B、19 C、25 D、169

查看试题解析

二、填空题

7. 化简： $\sqrt{\frac{2}{3}}$ × $\sqrt{\frac{27}{8}}$ = ．

查看试题解析
8. 如图，矩形ABCD中，AB＝3，AD＝1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于M，则点M的表示的数为．

查看试题解析
9. 如图，函数 $y ＝ 2 x$ 和 $y ＝ a x + 4$ 的图象交于点 $A (3 ， m)$ ，则不等式 $2 x < a x + 4$ 的解集是．

查看试题解析
10. 已知函数y=3x的图象经过点A(-1,y₁),点B(-2,y₂),则y₁y₂(填“>”或“<”或“=”).

查看试题解析
11. 如图，有两颗树，一颗高10米，另一颗高4米，两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢，问小鸟至少飞行米.

查看试题解析
12. 一次函数 $y = k x + b$ （k，b为常数， $k \neq 0$ )的图象如图所示，根据图象信息可得到关于x的方程 $k x + b = 4$ 的解为.

查看试题解析
13. 如图，菱形 $A B C D$ 中， $A E$ 垂直平分 $B C$ ，垂足为 $E$ ， $A B ＝ 2 c m$ ．那么菱形 $A B C D$ 的对角线 $B D$ 的长是 $c m$ ．

查看试题解析
14. 小明用四根长度相同的木条制作了能够活动的菱形学具，他先活动学具成为图1所示菱形，并测得 $∠ B ＝ 60 °$ ，接着活动学具成为图2所示正方形，并测得正方形的对角线 $A C ＝ 40 c m$ ，则图1中对角线AC的长为 $c m$ ．

查看试题解析

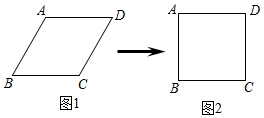
三、综合题

15. 化简： $(3 \sqrt{12} - 2 \sqrt{\frac{1}{3}} + \sqrt{48}) \div 2 \sqrt{3}$ ．

查看试题解析
16. 计算： $(\sqrt{2} + 1) (\sqrt{2} - 1) + {(\sqrt{3} - 2)}^{2}$ ．

查看试题解析
17. 已知 $x = 2 - \sqrt{3}$ ， $y ＝ 2 + \sqrt{3}$ ，求代数式 $x^{2} - y^{2}$ 的值．

查看试题解析
18. 已知，正比例函数 $y ＝ k_{1} x$ 的图象与一次函数 $y ＝ k_{2} x - 3$ 的图象交于点 $P (3 ， - 6)$ ．

(1)、求 $k_{1}$ ， $k_{2}$ 的值；

(2)、求一次函数 $y ＝ k_{2} x - 3$ 的图象与 $y ＝ 3$ ， $x ＝ 3$ 围成的三角形的面积．

查看试题解析
19. 问题情境：在综合与实践课上，同学们以“已知三角形三边的长度，求三角形面积”为主题开展数学活动，小颖想到借助正方形网格解决问题．图 1，图 2 都是 8×8 的正方形网格，每个小正方形的边长均为 1，每个小正方形的顶点称为格点．

操作发现：小颖在图 1 中画出△ABC，其顶点 A，B，C 都是格点，同时构造正方形 BDEF，使它的顶点都在格点上，且它的边 DE，EF 分别经过点 C，A，她借助此图求出了△ABC 的面积．

(1)、在图1中，小颖所画的△ABC的三边长分别是 AB＝， BC＝， AC
＝；△ABC 的面积为．

(2)、已知△ABC 中，AB＝ $\sqrt{10}$ ，BC＝2 $\sqrt{5}$ ，AC＝5 $\sqrt{2}$ ，请你根据小颖的思路，在图2的正方形网格中画出△ABC，并直接写出△ABC的面积．

查看试题解析
20. 甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：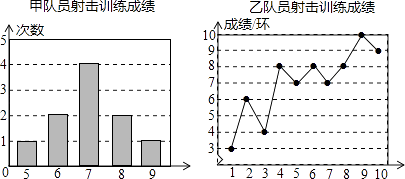
根据以上信息，整理分析数据如下：
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c

(1)、写出表格中a，b，c的值；

(2)、分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？

查看试题解析
21. 如图，过点A（2，0）的两条直线 $l_{1}$ ， $l_{2}$ 分别交y轴于B，C，其中点B在原点上方，点C在原点下方，已知AB= $\sqrt{13}$ .

(1)、求点B的坐标；

(2)、若△ABC的面积为4，求 $l_{2}$ 的解析式.

查看试题解析
22. 如图，在平行四边形 $A B C D$ 中， $E$ 是 $A D$ 边上的中点，连接 $B E$ ，并延长 $B E$ 交 $C D$ 的延长线于点 $F$ ．证明： $F D ＝ A B$ ．

查看试题解析
23. 某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷数量收取印刷费．甲乙两厂的印刷费用y（千元）与证书数量x（千个）的函数关系图象分别如图中甲、乙所示．

(1)、填空：甲厂的制版费是千元，当x≤2（千个）时乙厂证书印刷单价是元/个；

(2)、求出甲厂的印刷费y_甲与证书数量x的函数关系式，并求出其证书印刷单价；

(3)、当印制证书8千个时，应选择哪个印刷厂节省费用，节省费用多少元？

查看试题解析
24. 如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．

(1)、求证：四边形BFCE是平行四边形；

(2)、若AD=10，DC=3，∠EBD=60°，则BE=时，四边形BFCE是菱形．

查看试题解析
25. 如图，直线 $y ＝ k x + 6$ 分别与 $x$ 轴、 $y$ 轴相交于点 $E$ 和点 $F$ ，点 $E$ 的坐标为 $(- 8 ， 0)$ ，点 $A$ 的坐标为 $(0 ， 3)$ ．

(1)、求 $k$ 的值；

(2)、若点 $P (x ， y)$ 是第二象限内的直线上的一个动点，当点 $P$ 运动过程中，试写出 $Δ O P A$ 的面积 $S$ 与 $x$ 的函数关系式，并写出自变量 $x$ 的取值范围；

(3)、探究：当 $P$ 运动到什么位置时， $Δ O P A$ 的面积为 $\frac{27}{8}$ ，并说明理由．

查看试题解析
26. 如图

(1)、感知：如图①，在正方形 $A B C D$ 中， $E$ 是 $A B$ 一点， $F$ 是 $A D$ 延长线上一点，且 $D F ＝ B E$ ，求证： $C E ＝ C F$ ；

(2)、拓展：在图①中，若 $G$ 在 $A D$ ，且 $∠ G C E ＝ 45 °$ ，则 $G E ＝ B E + G D$ 成立吗？为什么？

查看试题解析

	平均成绩/环	中位数/环	众数/环	方差
甲	a	7	7	1.2
乙	7	b	8	c