广东省肇庆市怀集县2018-2019学年八年级上学期期末考试试卷

试卷更新日期：2020-05-18 类型：期末考试

进入出卷网下载

一、选择题

1. 下列线段长能构成三角形的是（）

A、3、4、8 B、2、3、6 C、5、6、11 D、5、6、10

查看试题解析
2. 如图所示的五角星是轴对称图形，它的对称轴共有（）

A、1条 B、3条 C、5条 D、无数条

查看试题解析
3. 在平面直角坐标系中，点P(2，﹣3)关于x轴的对称点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 一个缺角的三角形ABC残片如图所示，量得∠A＝60°，∠B＝75°，则这个三角形残缺前的∠C的度数为（）

A、75° B、60° C、45° D、40°

查看试题解析
5. 计算（-2b）³的结果是（）

A、 $- 8 b^{3}$ B、 $8 b^{3}$ C、 $- 6 b^{3}$ D、 $6 b^{3}$

查看试题解析
6. 下列多项式能用完全平方公式进行因式分解的是（）

A、a²﹣1 B、a²+4 C、a²+2a+1 D、a²﹣4a﹣4

查看试题解析
7. 如图，在△ABC中，∠B＝50°，∠A＝30°，CD平分∠ACB ， CE⊥AB于点E ，则∠DCE的度数是（）

A、5° B、8° C、10° D、15°

查看试题解析
8. 如图，要测量河两岸相对的两点 $A$ 、 $B$ 的距离，先在 $A B$ 的垂线 $B F$ 上取两点 $C$ 、 $D$ ，使 $C D = B C$ ，再作 $B F$ 的垂线 $D E$ ，使 $A$ 、 $C$ 、 $E$ 在一条直线上，可以说明 $Δ E D C ≅ Δ A B C$ ，得 $E D = A B$ ，因此测得 $E D$ 的长就是 $A B$ 的长，判定 $Δ E D C ≅ Δ A B C$ 的理由是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $H L$

查看试题解析
9. 化简 $\frac{m^{2} - 3 m}{9 - m^{2}}$ 的结果是（）

A、 $\frac{m}{m - 3}$ B、 $\frac{m}{3 - m}$ C、 $- \frac{m}{m + 3}$ D、 $\frac{m}{m + 3}$

查看试题解析
10. 某工厂计划x天内生产120件零件，由于采用新技术，每天增加生产3件，因此提前2天完成计划，列方程为（）

A、 $\frac{120}{x - 2} - \frac{120}{x} = 2$ B、 $\frac{120}{x} = \frac{120}{x + 2} - 3$ C、 $\frac{120}{x + 2} = \frac{120}{x} - 3$ D、 $\frac{120}{x} = \frac{120}{x - 2} - 3$

查看试题解析

二、填空题

11. 计算： $2^{- 1} - 2^{0} =$ ．

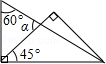
查看试题解析
12. 八边形的外角和等于°．

查看试题解析
13. 分解因式：x²-2x+1=.

查看试题解析
14. 要使分式 $\frac{x + 2}{x - 1}$ 有意义，则x应满足条件．

查看试题解析
15. 将一副直角三角板，按如图所示叠放在一起，则图中∠α的度数是．

查看试题解析
16. 如图，△ABC≌△DCB，∠DBC＝35°，则∠AOB的度数为.

查看试题解析
17. 如图，等边△ABC的周长为18cm ， BD为AC边上的中线，动点P ， Q分别在线段BC ， BD上运动，连接CQ ， PQ ，当BP长为cm时，线段CQ+PQ的和为最小．

查看试题解析

三、综合题

18. 计算： $(a + b) (a - b) + {(2 a - b)}^{2}$

查看试题解析
19. 先化简，再求值： $\frac{a + 1}{a} \div \frac{a^{2} - 1}{a^{2}}$ ，其中a=2019．

查看试题解析
20. 如图，在△ABC中，AB＝AC，D为BC边上一点，∠B＝30°，∠DAB＝45°.

(1)、求∠DAC的度数；

(2)、求证：DC＝AB.

查看试题解析
21. 如图，在Rt△ABC中，∠C＝90°，∠A＝30°．

(1)、尺规作图：作∠B的平分线BD交AC于点D；（不写作法，保留作图痕迹）

(2)、若DC＝2，求AC的长．

查看试题解析
22. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形ABC(顶点是网格线的交点的三角形)的顶点A，C的坐标分别为(﹣4，5)，(﹣1，3).

(1)、请作出△ABC关于y轴对称的△A₁B₁C₁；

(2)、△A₁B₁C₁的面积是.

查看试题解析
23. 山地自行车越来越受中学生的喜爱．一网店经营的一个型号山地自行车，今年一月份销售额为30000元，二月份每辆车售价比一月份每辆车售价降价100元，若销售的数量与上一月销售的数量相同，则销售额是27000元．

(1)、求二月份每辆车售价是多少元？

(2)、为了促销，三月份每辆车售价比二月份每辆车售价降低了10%销售，网店仍可获利35%，求每辆山地自行车的进价是多少元？

查看试题解析
24. 已知，如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD于Q．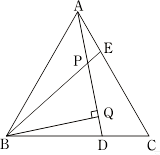

(1)、求证：BE=AD；

(2)、求∠BPQ的度数；

(3)、若PQ=3，PE=1，求AD的长．

查看试题解析
25. 如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．

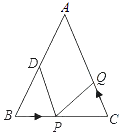(1)、如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

(2)、若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？

查看试题解析