广东省汕头市潮南区两英镇2018-2019学年八年级下学期期末考试试卷
试卷更新日期:2020-05-18 类型:期末考试
一、选择题
-
1. 的平方根是( )A、 B、 C、 D、2. 如果△ABC的三个顶点A , B , C所对的边分别为a , b , c , 那么下列条件中,不能判断△ABC是直角三角形的是( )A、∠A=25°,∠B=65° B、∠A:∠B:∠C=2:3:5 C、a:b:c= : : D、a=6,b=10,c=123. 某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲
乙
丙
丁
平均数/环
9.5
9.5
9.5
9.5
方差/环2
5.1
4.7
4.5
5.1
请你根据表中数据选一人参加比赛,最合适的人选是( )
A、甲 B、乙 C、丙 D、丁4. 如图,在平行四边形ABCD中,CE⊥AB , E为垂足.如果∠BCE=28°,则∠D=( )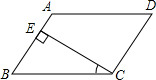 A、28° B、38° C、52° D、62°5. 如图,∠ABC=∠ADC=90°,E是AC的中点,则( )
A、28° B、38° C、52° D、62°5. 如图,∠ABC=∠ADC=90°,E是AC的中点,则( ) A、∠1>∠2 B、∠1=∠2 C、∠1<∠2 D、∠1与∠2大小关系不能确定6. 若 (n为整数),则m的值可以是( )A、 B、12 C、18 D、247. 如图,在△ABC中,∠B=45°,∠ACB=60°,AB=16,AD⊥BC , 垂足为D , ∠ACB的平分线交AD于点E , 则AE的长为( )
A、∠1>∠2 B、∠1=∠2 C、∠1<∠2 D、∠1与∠2大小关系不能确定6. 若 (n为整数),则m的值可以是( )A、 B、12 C、18 D、247. 如图,在△ABC中,∠B=45°,∠ACB=60°,AB=16,AD⊥BC , 垂足为D , ∠ACB的平分线交AD于点E , 则AE的长为( )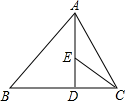 A、 B、4 C、 D、68. 已知一次函数y=kx+b随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )A、
A、 B、4 C、 D、68. 已知一次函数y=kx+b随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )A、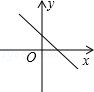 B、
B、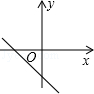 C、
C、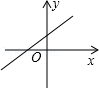 D、
D、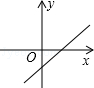 9. 如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF , 则添加下列条件①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF . 可以判定四边形BEDF是菱形的条件有( )
9. 如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF , 则添加下列条件①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF . 可以判定四边形BEDF是菱形的条件有( )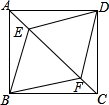 A、1个 B、2个 C、3个 D、4个10. 如图,直线y=-x+2分别交x轴、y轴于点A,B,点D在BA的延长线上,OD的垂直平分线交线段AB于点C.若△OBC和△OAD的周长相等,则OD的长是( )
A、1个 B、2个 C、3个 D、4个10. 如图,直线y=-x+2分别交x轴、y轴于点A,B,点D在BA的延长线上,OD的垂直平分线交线段AB于点C.若△OBC和△OAD的周长相等,则OD的长是( ) A、2 B、2 C、 D、4
A、2 B、2 C、 D、4二、填空题
-
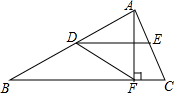
11. 已知m+3n的值为2 ,则 ﹣m﹣3n的值是 .12. 若一组数据4,a,7,8,3的平均数是5,则这组数据的中位数是 .13. 如图,在△ABC中,点D , E分别是边AB , AC的中点,AF⊥BC , 垂足为点F , ∠ADE=30°,DF=3,则AF的长为 .
 14. 已知三角形三边长分别为 , , ,则此三角形的最大边上的高等于.15. 如图,E是矩形ABCD的对角线的交点,点F在边AE上,且DF=DC , 若∠ADF=25°,则∠ECD=°.
14. 已知三角形三边长分别为 , , ,则此三角形的最大边上的高等于.15. 如图,E是矩形ABCD的对角线的交点,点F在边AE上,且DF=DC , 若∠ADF=25°,则∠ECD=°. 16. 一次函数y=kx﹣2的图象经过第一、三、四象限,且与两坐标轴围成的三角形的面积等于4,则k的值等于 .
16. 一次函数y=kx﹣2的图象经过第一、三、四象限,且与两坐标轴围成的三角形的面积等于4,则k的值等于 .三、综合题
-
17. 计算:18. 已知a= , 求 的值.
19. 如图,将平行四边形ABCD的AD边延长至点E , 使DE= AD , 连接CE , F是BC边的中点,连接FD . 求证:四边形CEDF是平行四边形. 20.
20.如图,在平行四边形ABCD中,AB<BC.
 (1)、利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);(2)、若BC=8,CD=5,则CE= .21. 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F , 连接CD .
(1)、利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);(2)、若BC=8,CD=5,则CE= .21. 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F , 连接CD .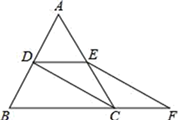 (1)、求证:DE=CF;(2)、求EF的长.22. 如图一次函数y=kx+b的图象经过点A和点B.
(1)、求证:DE=CF;(2)、求EF的长.22. 如图一次函数y=kx+b的图象经过点A和点B. (1)、写出点A和点B的坐标并求出k、b的值;(2)、求出当x= 时的函数值.23. 如图,正方形ABCD中,M为BC上的点,E是AD的延长线的点,且AE=AM , 过E作EF⊥AM垂足为F , EF交DC于点N .
(1)、写出点A和点B的坐标并求出k、b的值;(2)、求出当x= 时的函数值.23. 如图,正方形ABCD中,M为BC上的点,E是AD的延长线的点,且AE=AM , 过E作EF⊥AM垂足为F , EF交DC于点N .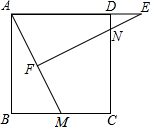 (1)、求证:AF=BM;(2)、若AB=12,AF=5,求DE的长.24. 春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售,并分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.(1)、让小王将水果全部售出共赚了215元,则小王共购进A、B水果各多少箱?(2)、若要求购进A水果的数量不得少于B水果的数量,则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润,此时最大利润是多少?25. 如图,在平行四边形ABCD中, ,延长DA于点E,使得 ,连接BE.
(1)、求证:AF=BM;(2)、若AB=12,AF=5,求DE的长.24. 春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售,并分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.(1)、让小王将水果全部售出共赚了215元,则小王共购进A、B水果各多少箱?(2)、若要求购进A水果的数量不得少于B水果的数量,则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润,此时最大利润是多少?25. 如图,在平行四边形ABCD中, ,延长DA于点E,使得 ,连接BE.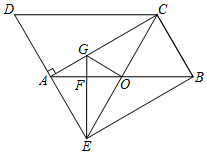 (1)、求证:四边形AEBC是矩形;(2)、过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若 , ,求 的面积.
(1)、求证:四边形AEBC是矩形;(2)、过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若 , ,求 的面积.