广东省茂名市电白区2018-2019学年八年级下学期期末考试试卷
试卷更新日期:2020-05-18 类型:期末考试
一、选择题
-
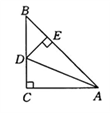
1. 下列各式从左到右的变形中,是因式分解的为( ).A、 B、 C、 D、2. 在下列各式 中,是分式的有( )A、2个 B、3个 C、4个 D、5个3. 下列关于x的方程中,是分式方程的是( ).A、 B、 C、 D、3x-2y=14. 如图所示.在△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,若AB=6 cm,则△DEB的周长为( )
 A、12 cm B、8 cm C、6 cm D、4 cm5. 下列变形不正确的是( )A、 B、 C、 D、6. 如图,在▱ABCD中,AC与BD交于点O,下列说法正确的是( )
A、12 cm B、8 cm C、6 cm D、4 cm5. 下列变形不正确的是( )A、 B、 C、 D、6. 如图,在▱ABCD中,AC与BD交于点O,下列说法正确的是( )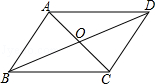 A、AC=BD B、AC⊥BD C、AO=CO D、AB=BC7. 已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )A、8或10 B、8 C、10 D、6或128. 如图,函数y=2x-4与x轴.y轴交于点(2,0),(0,-4),当-4<y<0时,x的取值范围是( )
A、AC=BD B、AC⊥BD C、AO=CO D、AB=BC7. 已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )A、8或10 B、8 C、10 D、6或128. 如图,函数y=2x-4与x轴.y轴交于点(2,0),(0,-4),当-4<y<0时,x的取值范围是( )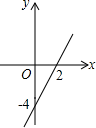 A、x<-1 B、-1<x<0 C、0<x<2 D、-1<x<29. 若不等式组 的解集为 ,则 的值等于( )A、 B、 C、2 D、410. 如图1,△ABC和△ADE都是等腰直角三角形,∠C和∠ADE都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2.两次旋转的角度分别为( )
A、x<-1 B、-1<x<0 C、0<x<2 D、-1<x<29. 若不等式组 的解集为 ,则 的值等于( )A、 B、 C、2 D、410. 如图1,△ABC和△ADE都是等腰直角三角形,∠C和∠ADE都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2.两次旋转的角度分别为( )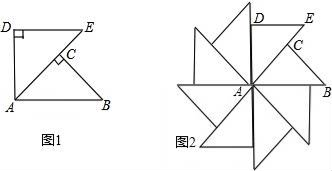 A、45°,90° B、90°,45° C、60°,30° D、30°,60°
A、45°,90° B、90°,45° C、60°,30° D、30°,60°二、填空题
-
11. 分解因式:a2+a= .12. 若分式 有意义,则 的取值范围是 .13. 一个多边形的内角和与外角和的比是4:1,则它的边数是 .14. 分式 与 的最简公分母是.15. 如图,在△ABC中,D,E分别是边AB,AC的中点,若BC=6,则DE= .
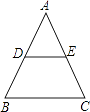 16. 如图,已知∠BAC=120º,AB=AC,AC的垂直平分线交BC于点D,则∠ADB=;
16. 如图,已知∠BAC=120º,AB=AC,AC的垂直平分线交BC于点D,则∠ADB=;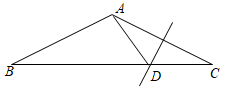 17. 在三个整式x2+2xy,y2+2xy,x2中,请你任意选出两个进行加(或减)运算,使所得整式可以因式分解,并进行因式分解.18. 解方程: - =1.19. 如图,已知▱ABCD.
17. 在三个整式x2+2xy,y2+2xy,x2中,请你任意选出两个进行加(或减)运算,使所得整式可以因式分解,并进行因式分解.18. 解方程: - =1.19. 如图,已知▱ABCD. (1)、作图:延长BC , 并在BC的延长线上截取线段CE , 使得CE=BC . (用尺规作图法,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连结AE , 交CD于点F , 求证:△AFD ≌ △EFC.20. 已知a,b,c是 的三边,且满足 ,试判断 的形状,并说明理由.21. 先化简,再求值:( )(x2-4),其中x= .22. 如图,在四边形 中, , , , , ,点 从点 出发,以 的速度沿 运动,点 从点 出发的同时,点 从点 出发,以 的速度向点 运动,当点 到达点 时,点 也停止运动,设点 、 运动的时间为 秒,从运动开始,当 取何值时, ?
(1)、作图:延长BC , 并在BC的延长线上截取线段CE , 使得CE=BC . (用尺规作图法,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连结AE , 交CD于点F , 求证:△AFD ≌ △EFC.20. 已知a,b,c是 的三边,且满足 ,试判断 的形状,并说明理由.21. 先化简,再求值:( )(x2-4),其中x= .22. 如图,在四边形 中, , , , , ,点 从点 出发,以 的速度沿 运动,点 从点 出发的同时,点 从点 出发,以 的速度向点 运动,当点 到达点 时,点 也停止运动,设点 、 运动的时间为 秒,从运动开始,当 取何值时, ?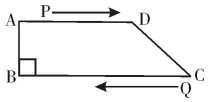 23. 如图, 是边长为2的等边三角形,将 沿直线 平移到 的位置,连接 .
23. 如图, 是边长为2的等边三角形,将 沿直线 平移到 的位置,连接 .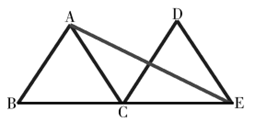 (1)、求 平移的距离;(2)、求 的长.24. 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)、求 平移的距离;(2)、求 的长.24. 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.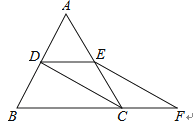 (1)、求证:DE=CF;
(1)、求证:DE=CF;
(2)、求EF的长;
25. 某汽车销售公司经销某品牌 款汽车,随着汽车的普及,其价格也在不断下降.今年5月份 款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的 款汽车,去年销售额为100万元,今年销售额只有90万元.(1)、今年5月份 款汽车每辆售价多少万元?(2)、为了增加收入,汽车销售公司决定再经销同品牌的 款汽车,已知 款汽车每辆进价为7.5万元, 款汽车每辆进价为6万元,公司预计用不多于105万元且不少于102万元的资金购进这两款汽车共15辆,有几种进货方案?(3)、按照(2)中两种汽车进价不变,如果 款汽车每辆售价为8万元,为打开 款汽车的销路,公司决定每售出一辆 款汽车,返还顾客现金 万元,要使(2)中所有的方案获利相同, 值应是多少?