吉林省长春市农安县2017-2018学年七年级下学期期末考试试卷

试卷更新日期：2020-05-18 类型：期末考试

进入出卷网下载

一、选择题

1. 方程﹣3x＝9的解是（）

A、x＝﹣3 B、x＝3 C、x＝﹣ $\frac{1}{3}$ D、x＝ $\frac{1}{3}$

查看试题解析
2. 若 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是方程3x+ay＝1的解，则a的值是（）

A、a＝1 B、a＝﹣1 C、a＝2 D、a＝﹣2

查看试题解析
3. 已知三角形两边长分别为3和8，则该三角形第三边的长可能是（　　）

A、3 B、5 C、8 D、11

查看试题解析
4. 如图所示的图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 能和正八边形一起铺满地面的是（　　）

A、正十边形 B、正六边形 C、正四边形 D、正三角形

查看试题解析
6. 如图，直线a∥b ．若∠1＝30°，∠2＝45°，则∠3的大小为（）

A、75° B、80° C、85° D、105°

查看试题解析
7. 如图，△ABC≌△CDA ，若AB＝3，BC＝4，则四边形ABCD的周长是（）

A、14 B、11 C、16 D、12

查看试题解析
8. 已知 ${\begin{array}{l} x + 2 y = 4 k \\ 2 x + y = 2 k + 1 \end{array}$ ，且 $- 1 < x - y < 0$ ，则k的取值范围为（）

A、 $- 1 < k < - \frac{1}{2}$ B、 $0 < k < \frac{1}{2}$ C、 $0 < k < 1$ D、 $\frac{1}{2} < k < 1$

查看试题解析

二、填空题

9. 不等式3x＞6的解集是

查看试题解析
10. 七边形的内角和是

查看试题解析
11. 如图，AD是△ABC的中线．若△ABD的面积是3，则△ABC的面积是．

查看试题解析
12. 如图，直线DE分别交△ABC边AC、AB于点D、E ，将△ABC沿DE翻折，使点A恰好与点C重合．若AB＝3，BC＝2，则△BCE的周长是．

查看试题解析
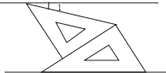
13.
如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是．

查看试题解析
14. 如图，将锐角三角形△ABC绕点B按顺时针方向旋转35°，得到△A′BC′．若A′C′⊥BC于点D ，则∠C的度数是．

查看试题解析
15. 解方程： $3 x - 6 (x - 1) = 3 - 2 (x + 3)$

查看试题解析
16. 解方程组： ${\begin{matrix} 3 x - 5 y = 3 \\ \frac{x}{2} - \frac{y}{3} = 1 \end{matrix}$ ．

查看试题解析
17. 图①、图②、图③是3×3的正方形网格，每个网格图中有3个小正方形己涂上阴影，请在余下的6个空白小正方形中，按下列要求涂上阴影：

(1)、在图①中选取1个空白小正方形涂上阴影，使4个阴影小正方形组成一个轴对称图形，但不是中心对称图形．

(2)、在图②中选取1个空白小正方形涂上阴影，使4个阴影小正方形组成一个中心对称图形，但不是轴对称图形．

(3)、在图③中选取2个空白小正方形涂上阴影，使5个阴影小正方形组成一个轴对称图形．（请将三个小题依次作答在图①、图②、图③中，均只需画出符合条件的一种情形）

查看试题解析
18. 解不等式组 ${\begin{array}{l} 5 x + 1 \geq 3 (x - 1) \\ 2 - x > \frac{3 - x}{2} \end{array}$ ，并将它的解集表示在如图所示的数轴上．

查看试题解析
19. 一个多边形的每一个内角都相等，并且每个外角都等于和它相邻的内角的 $\frac{2}{3}$ ，求这个多边形的边数及内角和.

查看试题解析
20. 如图，将△ABC沿射线AB的方向平移2个单位到△DEF的位置，点A、B、C的对应点分别点D、E、F．

(1)、直接写出图中与AD相等的线段．

(2)、若AB＝3，则AE＝．

(3)、若∠ABC＝75°，求∠CFE的度数．

查看试题解析
21. A ， B两地之间路程是200千米，甲、乙两车同时从A地出发，沿同一路线匀速行驶，前往B地，甲车行驶到B地后立即返回．已知甲车速度是乙车速度的1.5倍，两车行驶2小时相遇．

(1)、求甲、乙两车的速度；

(2)、当两车相遇时，求甲车距B地的路程．

查看试题解析
22. 如图

(1)、探究：如图①，在△ABC中，∠ACB＝90°，CD⊥AB于点D ，若∠B＝30°，则∠ACD的度数是度；

(2)、拓展：如图②，∠MCN＝90°，射线CP在∠MCN的内部，点A、B分别在CM、CN上，分别过点A、B作AD⊥CP、BE⊥CP ，垂足分别为D、E ，若∠CBE＝70°，求∠CAD的度数；

(3)、应用：如图③，点A、B分别在∠MCN的边CM、CN上，射线CP在∠MCN的内部，点D、E在射线CP上，连接AD、BE ，若∠ADP＝∠BEP＝60°，则∠CAD+∠CBE+∠ACB＝度．

查看试题解析

23. 某电器超市销售每台进价分别为200元，170元的A，B两种型号的电风扇，表中是近两周的销售情况：

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	3台	5台	1800元
第二周	4台	10台	3100元

(进价、售价均保持不变，利润＝销售收入－进货成本)

(1)、求A，B两种型号的电风扇的销售单价.

(2)、若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，则A种型号的电风扇最多能采购多少台？

(3)、在(2)的条件下，超市销售完这30台电风扇能否实现利润为1400元的目标？若能，请给出相应的采购方案；若不能，请说明理由.

查看试题解析

24. 如图，在△ABC中，∠CBD、∠BCE是△ABC的外角，BP平分∠ABC ， CP平分∠ACB ， BQ平分∠CBD ， CQ平分∠BCE ．

(1)、∠PBQ的度数是， ∠PCQ的度数是；

(2)、若∠A＝70°，求∠P和∠Q的度数；

(3)、若∠A＝α，则∠P＝， ∠Q＝（用含α的代数式表示）．

查看试题解析