吉林省长春市宽城区2018-2019学年七年级下学期期末考试试卷

试卷更新日期：2020-05-18 类型：期末考试

进入出卷网下载

一、选择题

1. $\sqrt{4}$ 的值是（）

A、4 B、2 C、﹣2 D、±2

查看试题解析
2. 若关于x的方程 $ax + 3 x + 6 = 0$ 的解是x=2，则a的值是（）

A、6 B、-6 C、4 D、4

查看试题解析
3. 1．在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列四个数中，与 $\sqrt{26}$ 最接近的整数是（）

A、4 B、5 C、6 D、7

查看试题解析
5. 某中学阅览室在装修过程中，准备用边长相等的正方形、正三角形两种地砖铺满地面，在每个顶点的周围正方形、正三角形地砖的块数分别是（）

A、1、2 B、2、1 C、2、2 D、2、3

查看试题解析
6. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一根竿子一条索，索比竿子长一托．折回索子再量竿，却比竿子短一托，问索和竿子各几何？”其大意为：“现有一根竿子和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对折后再去量竿，就比竿短5尺．问绳索和竿子各多少尺？”设绳索长x尺，竿子长y尺，下列所列方程组正确的是（）

A、 ${\begin{matrix} y - x = 5 \\ y - \frac{1}{2} x = 5 \end{matrix}$ B、 ${\begin{matrix} y - x = 5 \\ \frac{1}{2} x - y = 5 \end{matrix}$ C、 ${\begin{matrix} x - y = 5 \\ \frac{1}{2} x - y = 5 \end{matrix}$ D、 ${\begin{matrix} x - y = 5 \\ y - \frac{1}{2} x = 5 \end{matrix}$

查看试题解析
7. 如图，在△ABC中，CD平分∠ACB交AB于点D，过点D作DE∥BC交AC于点E．若∠A=54°，∠B=48°，则∠CDE的大小为（）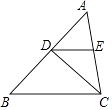

A、44° B、40° C、39° D、38°

查看试题解析
8. 如图，将△ABC绕点C按顺时针方向旋转90°得到△EDC．若点A、D、E在同一条直线上， $∠ ACB = 25 °$ ，则 $∠$ ADC的大小为（）

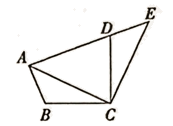A、60° B、5° C、70° D、75°

查看试题解析

二、填空题

9. 化简： $\sqrt{12}$ =； $\sqrt{{(5 - 7)}^{2}}$ × $\sqrt{{(2 - 6)}^{2}}$ = ．

查看试题解析
10. 已知a，b，c是△ABC的三边长，a，b满足|a﹣7|+（b﹣1）²=0，c为奇数，则c= ．

查看试题解析
11. 如图，△ABC≌△DCB．若 $∠$ A=80°， $∠$ DBC=40°，则 $∠$ DCA的大小为度．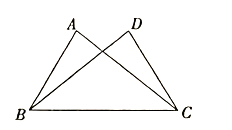

查看试题解析
12. 如图，点E是△ABC的边BC延长线上一点，ED⊥AB于点D．若 $∠$ A=30°， $∠$ E=40°，则 $∠$ ACE的大小为度．

查看试题解析
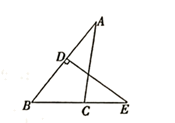13. 如图，在五边形ABCDE中， $∠ A + ∠ B + ∠ C = 300 °$ ，DP、CP分别平分 $∠$ EDC、 $∠$ BCD，则 $∠ P$ 的大小为度．

查看试题解析
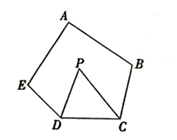14. 如图，某住宅小区内有一长方形地，若在长方形地内修筑同样宽的小路（图中阴影都分），余下部分绿化，小路的宽均为2m，则绿化的面积为 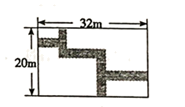$m^{2}$ ．

查看试题解析

三、综合题

15. 计算： $\sqrt{16} + \sqrt[3]{- 27} - \sqrt{\frac{9}{25}}$ ．

查看试题解析
16. 一个多边形的内角和比它外角和的3倍少180°，求这个多边形的边数．

查看试题解析
17. 小明在解不等式 $\frac{x + 4}{3} - \frac{3 x - 1}{2} \geq 1$ 的过程中出现了不正确，解答过程如下：

(1)、小明的解答过程是从第步开始出现不正确的．

(2)、请写出此题正确的解答过程．

查看试题解析
18. 图①、图②、图③均是 $4 \times 4$ 的正方形网格，每个小正方形的顶点称为格点，△ABC的三个顶点都在格点上．

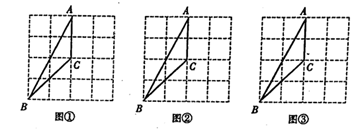(1)、在图①中，画出一个以点C为对称中心，与△ABC成中心对称的格点三角形．

(2)、在图②中，画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形．

(3)、在图③中，画出△ABC绕着点C按顺时针方向旋转90°后的格点三角形．

查看试题解析
19. 用一条长为18cm的细绳围成一个等腰三角形.

(1)、如果腰长是底边长的2倍，求三角形各边的长.

(2)、能围成有一边的长是4cm的等腰三角形吗？若能，求出其他两边的长；若不能，请说明理由.

查看试题解析
20. 如图，△ABC≌△DBE，点D在边AC上，BC与DE交于点P．已知 $∠ ABE = 162 °$ ， $∠ DBC = 30 °$ ， $AD = DC = 2.5$ ， $BC = 4$ .

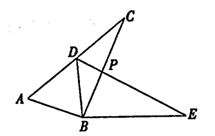(1)、求∠CBE的度数．

(2)、求△CDP与△BEP的周长和．

查看试题解析
21. 若∠A与∠B的两边分别垂直，请判断这两个角的数量关系．

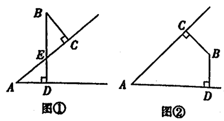(1)、如图①，∠A与∠B的数量关系是，如图②，∠A与∠B的数量关系是.

(2)、请从图①或图②中选择一种情况说明理由。

查看试题解析
22. 如图

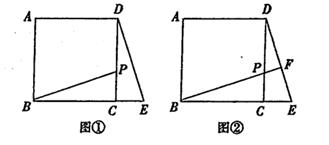(1)、探究：如图①，在正方形ABCD中，点P在边CD上（不与点C、D重合），连结BP．将△BCP绕点C顺时针旋转至△DCE，点B的对应点是点D，旋转的角度是度．

(2)、应用：将图①中的BP延长交边DE于点F，其它条件不变，如图②．求∠BFE的度数．

(3)、拓展：如图②，若DP=2CP，BC=3，则四边形ABED的面积是.

查看试题解析
23. 为提高市民的环保意识，倡导“节能减排，绿色出行”，某市计划在城区投放一批“共享单车”这批单车分为A，B两种不同款型，其中A型车单价400元，B型车单价320元．

(1)、今年年初，“共享单车”试点投放在某市中心城区正式启动．投放A，B两种款型的单车共100辆，总价值36800元．试问本次试点投放的A型车与B型车各多少辆？

(2)、试点投放活动得到了广大市民的认可，该市决定将此项公益活动在整个城区全面铺开．按照试点投放中A，B两车型的数量比进行投放，且投资总价值不低于184万元．请问城区10万人口平均每100人至少享有A型车与B型车各多少辆？

查看试题解析
24. 如图，∠MON=90°，点A、B分别在OM、ON上运动（不与点O重合）．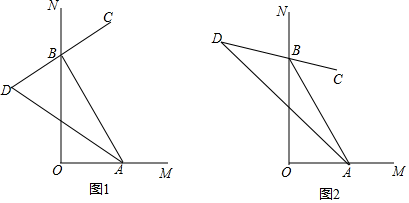

(1)、如图①，BC是∠ABN的平分线，BC的反方向延长线与∠BAO的平分线交于点D．
若∠BAO=60°，则∠D的大小为度，

(2)、猜想：∠D的度数是否随A、B的移动发生变化？请说明理由．

(3)、如图②，若∠ABC= $\frac{1}{3}$ ∠ABN， ∠BAD= $\frac{1}{3}$ ∠BAO，则∠D的大小为度，若∠ABC= $\frac{1}{n}$ ∠ABN， ∠BAD= $\frac{1}{n}$ ∠BAO，则∠D的大小为度（用含n的代数式表示）．

查看试题解析